Bisher haben wir folgende Schritte durchgeführt:
Überführung der allgemeinen Differentialgleichung mit dem
instationären Term, dem Diffusionsterm und dem Quellterm in eine
Diskretisierungsgleichung. Die bisherige Ableitung für Wärmeleitung
mit Temperatur ![]() und Wärmeleitfähigkeit
und Wärmeleitfähigkeit ![]() kann einfach
umgeschrieben werden für eine allgemeine Variable
kann einfach
umgeschrieben werden für eine allgemeine Variable ![]() und ihren
Diffusionskoeffizienten
und ihren
Diffusionskoeffizienten ![]() . Der bisher weggelassene
Konvektionsterm wird hinzugenommen. Die Lösungsmethoden für
algebraische Gleichungen können weiter verwendet werden, solange die
Hinzunahme des Konvektionsterms die Form der Diskretisierungsgleichung
nicht verändert.
. Der bisher weggelassene
Konvektionsterm wird hinzugenommen. Die Lösungsmethoden für
algebraische Gleichungen können weiter verwendet werden, solange die
Hinzunahme des Konvektionsterms die Form der Diskretisierungsgleichung
nicht verändert.
Konvektion wird durch Strömung eines Fluids verursacht. In diesem
Kapitel suchen wir eine Lösung für ![]() in einem gegebenen
Strömungsfeld (d.h. gegebene Geschwindigkeiten und Dichte).
in einem gegebenen
Strömungsfeld (d.h. gegebene Geschwindigkeiten und Dichte).
Obwohl Konvektion der einzige neue Term ist, ist seine Formulierung
nicht trivial. Konvektion ist untrennbar mit Diffusion verbunden; beide
Terme müssen daher zusammen behandelt werden. Diffusion ist hier im
allgemeinen Sinn gemeint: der Diffusionsstrom der allgemeinen Variablen ![]() ist
ist
![]() . Die allgemeine
Transportgleichung enthält den Term
. Die allgemeine
Transportgleichung enthält den Term
![]() ,
der als Diffusionsterm bezeichnet wird (Beachte: Summation über
,
der als Diffusionsterm bezeichnet wird (Beachte: Summation über ![]() ,
daher Summe aus 3 Komponenten). Gleiches gilt für den Konvektionsterm
,
daher Summe aus 3 Komponenten). Gleiches gilt für den Konvektionsterm
![]() .
.
Das Strömungsfeld muß die Kontinuitätsgleichung erfüllen:
Die allgemeine Differentialgleichung
kann umgeschrieben werden zu
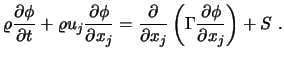 |
(5.3) |