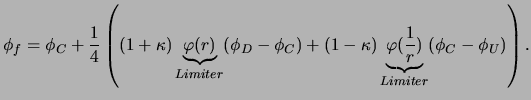 |
(5.67) |
Formal an das nichtlimitierte Schema (5.57) angelehnt,
läßt sich ein allgemeines TVD-Schema für die Interpolation der
zellzentralen Variablen auf die Zellgrenzflächen formulieren:
das MUSCL-Schema (Monotonic Upstream Scheme for Conservation
Laws, van Leer, 1979).
Dabei werden zusätzlich zwei Terme quasi als Dämpfungsterme (Limiter) eingefügt.
Die Limitierung wird durch den funktionalen Zusammenhang von ![]() und
und ![]() bestimmt. Um die oben erwähnte Forderung nach Begrenzung
der Totalen Variation erfüllen zu können, muß die
Limitierungsfunktion
bestimmt. Um die oben erwähnte Forderung nach Begrenzung
der Totalen Variation erfüllen zu können, muß die
Limitierungsfunktion
![]() innerhalb des schraffierten
Bereichs in Abbildung 32 liegen.
innerhalb des schraffierten
Bereichs in Abbildung 32 liegen.
Die Einführung der dimensionslosen Variablen
![]() und
und ![]()
![$\displaystyle \tilde{\phi}_f=\tilde{\phi}_C+\frac{1}{4}\tilde{\phi}_C
\left[ (1+\kappa)\frac{1}{r}\varphi (r)+(1-\kappa)\varphi (\frac{1}{r})
\right] . $](img704.png)
An dieser Stelle sollen symmetrische Limitierungsschemata betrachtet werden, die der Gleichung
genügen und somit die Gradienten auf beiden Seiten in gleicher Weise
behandeln.
Unter dieser Annahme vereinfacht sich das Schema erheblich und der
Rechenaufwand bei der Anwendung symmetrischer Verfahren ist erheblich
geringer. Der Parameter ![]() aus Gleichung (5.67)
fällt weg und es bleibt
schließlich die Gleichung für ein sehr einfaches Schema, das nur durch
unterschiedliche Funktionen
aus Gleichung (5.67)
fällt weg und es bleibt
schließlich die Gleichung für ein sehr einfaches Schema, das nur durch
unterschiedliche Funktionen
![]() variiert wird:
variiert wird:
Aufgrund der Normierung ergeben sich einige anschauliche
Zwangsbedingungen für die Monotonie des Verfahrens, die äquivalent
zu den mathematisch geforderten
Bedingungen sind. Zur Verdeutlichung sind in Abbildung 33
die Verteilungen der normierten Größen
![]() für einen
monotonen Verlauf (links,
für einen
monotonen Verlauf (links, ![]() ) und das Auftreten einer Extremstelle
(rechts,
) und das Auftreten einer Extremstelle
(rechts, ![]() ) dargestellt.
Im Fall einer aufgetretenen Extremstelle muß gelten:
) dargestellt.
Im Fall einer aufgetretenen Extremstelle muß gelten:
| (5.71) |
| (5.72) |
Unter der Beachtung aller Forderungen an
![]() aus
Abbildung 32 und aus Gleichung (5.69) ergibt
sich die allgemeine Formulierung für das MUSCL-Schema:
aus
Abbildung 32 und aus Gleichung (5.69) ergibt
sich die allgemeine Formulierung für das MUSCL-Schema:
| (5.73) |
| (5.74) |
| (5.75) |
Bei der Umsetzung des MUSCL-Verfahrens wird diese Beziehung in die dimensionsbehaftete Variante von Gleichung (5.70) eingesetzt.