 |
Approximierungsverfahren höherer Ordnung basieren auf der Interpolation durch Polynome höherer Ordnung. Derartige Kurven weisen eine proportional zur Ordnung steigende Anzahl von lokalen Extremwerten auf. Die Extremwerte wirken sich auf das Ergebnis eines numerischen Lösungsverfahrens derart aus, daß in den Profilen Schwankungen auftreten. So treten auch bei QUICK Oszillationen in der Lösung auf, die durch lokale Extremwerte der Näherungsparabel induziert werden. Dieser Effekt tritt besonders bei steilen Gradienten auf und ist ausschlaggebend dafür, daß der Gitterabstand bei den nichtlimitierten Verfahren höherer Ordnung nicht zu groß gewählt werden darf.
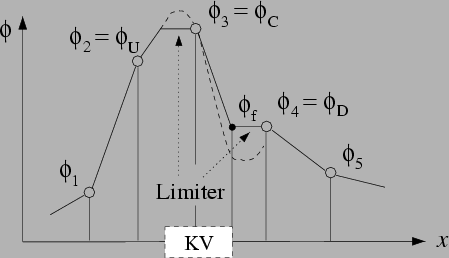
Die Idee der limitierten Differenzenschemata besteht darin, die Oszillationen begünstigenden Extremwerte durch vorgegebene Limits quasi abzuschneiden. In Abbildung 31 ist gezeigt, wie auftretende Schwingungen durch lokale Verminderung der Ordnung gedämpft werden können. Auf diese Weise sollen Verfahren höherer Ordnung wie beispielsweise QUICK zu stabilen Ergebnissen gezwungen werden. Da sich eine solche Limitierung nicht a priori einstellen läßt, sondern an jeder Stelle immer von der aktuellen Lösung bestimmt ist, sind limitierte Differenzenschemata grundsätzlich nichtlinear. Die Vermeidung von Oszillationen wird letztlich durch das Inkaufnehmen von lokalen Verminderungen der Approximationsordnung und ein nichtlineares Verfahren erreicht.
Harten beschrieb 1983 Anforderungen an limitierte Schemata. Verfahren, die den Zweck verfolgen, Oszillationen zu vermeiden und somit zwischen den Stützwerten monoton zu verlaufen, müssen zwei Bedingungen erfüllen:
Formal können diese Forderungen durch die Beschränkung der ''Totalen Variation'' über einem Intervall eingehalten werden. Deshalb heißt die Gruppe der limiterten Differenzenverfahren auch TVD-Verfahren (Total Variation Diminishing). Kontrolliert wird dabei die Monotonieeigenschaft der zweiten Ableitung.
Die Totale Variation von ![]() über ein Intervall ist definiert als
über ein Intervall ist definiert als
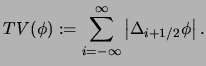 |
(5.63) |
| (5.64) |
Bezogen auf eine eindimensionale skalare Erhaltungsgleichung für
![]() vom Typ
vom Typ