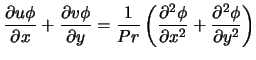 |
(5.78) |
Die Erweiterung der eindimensional definierten Differenzenschemata auf mehrdimensionale Anwendungen ist nicht trivial. Insbesondere in Bereichen, in denen Stromlinien die Gitterlinien unter ungünstigen Winkeln schneiden, treten sowohl numerische Difffusion als auch numerische Oszillationen in verstärktem Maße auf.
Zum Vergleich der unterschiedlichen Schemata wird auf einen Testfall zurückgegriffen, der Gegenstand eines 1982 von Smith und Hutton organisierten Workshops über Konvektionsschemata war. Hier galt es, in einem Rechengebiet mit vollständig vorgegebenem Geschwindigkeitsfeld eine Transportgleichung mit Konvektions- und Diffusionsanteil zu lösen. Sowohl das Geschwindigkeitsfeld als auch die Randbedingungen für die Transportgleichung sind so gewählt, daß sie hohe Anforderungen an das Konvektionssschema stellen und Bereiche mit unterschiedlichen Winkeln zwischen Stromlinien und Gitterlinien auftreten. Gelöst werden sollte die Gleichung
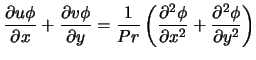 |
(5.78) |
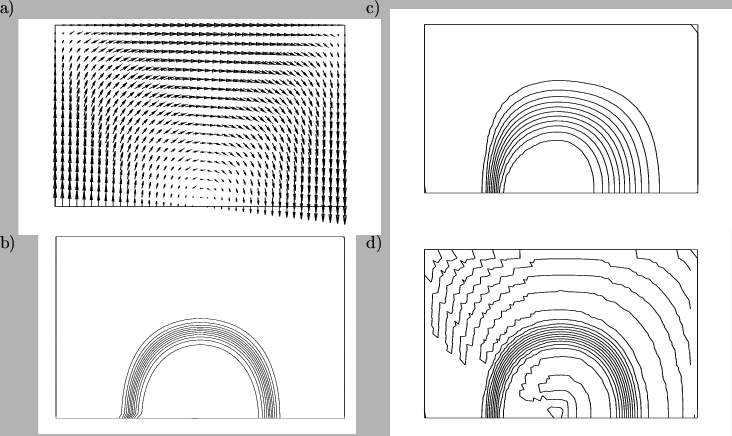 |
Das Geschwindigkeitsfeld ist gegeben. In Abbildung 37a oben sind die Geschwindigkeitsvektoren als Pfeile dargestellt, es ist
| (5.79) |
Die Randbedingungen für ![]() lauten:
lauten:
| oben, links und rechts: | |||
| unten: | |||
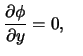 |
Dieses Problem sollte auf einem äquidistanten Gitter mit
![]() Gitterpunkten gelöst werden. Es gibt zwei Fälle:
Gitterpunkten gelöst werden. Es gibt zwei Fälle:
![]() und
und ![]() . Die Zell-Peclet-Zahl beträgt dann
. Die Zell-Peclet-Zahl beträgt dann ![]() bzw.
bzw. ![]() .
Ein Isolinienbild mit der exakten Lösung ist in
Abbildung 37b dargestellt.
.
Ein Isolinienbild mit der exakten Lösung ist in
Abbildung 37b dargestellt.
Im allgemeinen wird das Profil am Ausgang des Rechengebiets für den
Vergleich verschiedener Differenzenverfahren anhand dieses Testfalls
herangezogen. Bei der vorgegebenen hohen Geschwindigkeit und der
geringen Diffusion kann
insbesondere bei ![]() die Fähigkeit unterschiedlicher Verfahren
getestet werden, Strömungen zu beschreiben, die fast ausschließlich
durch Konvektion gekennzeichnet sind. Zu erwarten ist am Ausgang ein
Profil, das mit steigender
die Fähigkeit unterschiedlicher Verfahren
getestet werden, Strömungen zu beschreiben, die fast ausschließlich
durch Konvektion gekennzeichnet sind. Zu erwarten ist am Ausgang ein
Profil, das mit steigender ![]() -Zahl identisch dem Eingangsprofil wird.
-Zahl identisch dem Eingangsprofil wird.
In den Abbildungen 38/39 sind die Verläufe der
Transportgröße ![]() am Austrittsquerschnitt für die beiden
untersuchten
am Austrittsquerschnitt für die beiden
untersuchten ![]() -Zahlen aufgetragen.
Hier wird wiederum deutlich, worin der große Nachteil des
Upwind-Schemas liegt. Durch die Überbewertung der Diffusion ergibt
sich ein viel zu flacher Übergang von großen zu kleinen Werten von
-Zahlen aufgetragen.
Hier wird wiederum deutlich, worin der große Nachteil des
Upwind-Schemas liegt. Durch die Überbewertung der Diffusion ergibt
sich ein viel zu flacher Übergang von großen zu kleinen Werten von
![]() . Alle Verfahren höherer Ordnung erweisen sich hier als
wesentlich leistungsfähiger.
. Alle Verfahren höherer Ordnung erweisen sich hier als
wesentlich leistungsfähiger.
Für die kleinere ![]() -Zahl von 500 im linken Bild sind keine
nennenswerten Unterschiede zwischen den einzelnen Schemata zu
beobachten. Bemerkenswert ist dabei vor allem das Verhalten des
QUICK-Schemas. Bei der vorliegenden Peclet-Zahl von
-Zahl von 500 im linken Bild sind keine
nennenswerten Unterschiede zwischen den einzelnen Schemata zu
beobachten. Bemerkenswert ist dabei vor allem das Verhalten des
QUICK-Schemas. Bei der vorliegenden Peclet-Zahl von ![]() , die weit
über der Stabilitätsgrenze dieses Verfahrens von
, die weit
über der Stabilitätsgrenze dieses Verfahrens von
![]() liegt, sind trotzdem keine Anzeichen von Instabilitäten zu erkennen.
Die semi-implizite Implementierung ermöglicht es, daß QUICK auch bei
weit größeren
liegt, sind trotzdem keine Anzeichen von Instabilitäten zu erkennen.
Die semi-implizite Implementierung ermöglicht es, daß QUICK auch bei
weit größeren ![]() -Zahlen gute Ergebnisse liefert. Ähnliches gilt
auch für die Approximation mit Zentraldifferenzen. Im rechten Bild dagegen bei
-Zahlen gute Ergebnisse liefert. Ähnliches gilt
auch für die Approximation mit Zentraldifferenzen. Im rechten Bild dagegen bei ![]() und
und ![]() zeichnen sich die
Charakteristiken der einzelnen Verfahren ab: Die Approximation mit QUICK
weist leichte Überschwinger in den Übergangsbereichen auf, die
Genauigkeit des Verfahrens ist jedoch bei der gewählten
Implementierung nach wie vor sehr gut.
zeichnen sich die
Charakteristiken der einzelnen Verfahren ab: Die Approximation mit QUICK
weist leichte Überschwinger in den Übergangsbereichen auf, die
Genauigkeit des Verfahrens ist jedoch bei der gewählten
Implementierung nach wie vor sehr gut.
Die beste Genauigkeit bringt wie erwartet das ENO-Verfahren.
Für beide ![]() -Zahlen liegen die Ergebnisse praktisch auf der exakten
Lösung. Für das Smith-and-Hutton-Problem erwies es sich nicht als
notwendig, eine höhere Approximationsordnung zu wählen.
-Zahlen liegen die Ergebnisse praktisch auf der exakten
Lösung. Für das Smith-and-Hutton-Problem erwies es sich nicht als
notwendig, eine höhere Approximationsordnung zu wählen.
Das Hybrid Schema (HS) zeigt für diesen Testfall keine
befriedigende Lösung. Da es sich für große ![]() -Zahlen immer mehr
dem Upwind-Schema nähert, ergeben sich für
-Zahlen immer mehr
dem Upwind-Schema nähert, ergeben sich für ![]() , vor allem
aber für
, vor allem
aber für ![]() kaum Unterschiede zum UDS.
kaum Unterschiede zum UDS.
In Abbildung 39 werden zwei unterschiedliche Varianten
von MUSCL untersucht:
zunächst eine symmetrische Variante mit
![]() und zum
Vergleich eine nicht symmetrische Variante, d.h. ein Schema, bei
dem auf die Verwendung der Symmetriebedingung (5.69)
verzichtet wurde. Beide Schemata vermeiden Schwingungen, unterscheiden
sich aber bei der Genauigkeit der Wiedergabe. Das nichtsymmetrische
Schema folgt der exakten Lösung bemerkenswert gut, während das
symmetrische dazu neigt, die Diffusion etwas zu groß einzuschätzen
und deshalb den Anstieg zu flach annimmt.
und zum
Vergleich eine nicht symmetrische Variante, d.h. ein Schema, bei
dem auf die Verwendung der Symmetriebedingung (5.69)
verzichtet wurde. Beide Schemata vermeiden Schwingungen, unterscheiden
sich aber bei der Genauigkeit der Wiedergabe. Das nichtsymmetrische
Schema folgt der exakten Lösung bemerkenswert gut, während das
symmetrische dazu neigt, die Diffusion etwas zu groß einzuschätzen
und deshalb den Anstieg zu flach annimmt.
Das ROE-Schema zeigt die geringste numerische Diffusion. Da die Kurve jedoch steiler steigt als die exakte Lösung, muß man hier von einem leichten Überschwingen sprechen.
 |
Anhand des Smith-and-Hutton-Problems kann
außerdem die Implementierung der Verfahren hinsichtlich der Anwendung
auf zweidimensionale Strömungen untersucht werden. Durch die einfache
Erweiterung der eindimensionalen Approximation auf die zweite
Raumrichtung ist insbesondere in den Bereichen, wo sich Stromlinien und
Gitterlinien unter
![]() schneiden, mit numerischen Fehlern zu
rechnen. Hier können in verstärktem Maße Oszillationen auftreten.
Zur Beobachtung dieses Effektes sind hier Isoliniendarstellungen für
schneiden, mit numerischen Fehlern zu
rechnen. Hier können in verstärktem Maße Oszillationen auftreten.
Zur Beobachtung dieses Effektes sind hier Isoliniendarstellungen für
![]() unter Berücksichtigung verschiedener Differenzenverfahren
dargestellt.
unter Berücksichtigung verschiedener Differenzenverfahren
dargestellt.
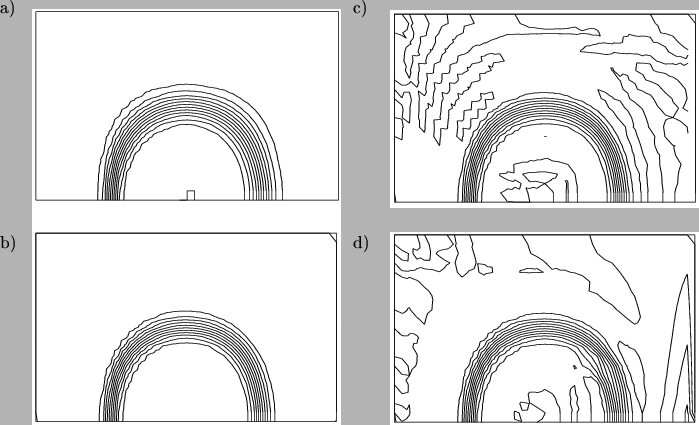
Abbildung 37c zeigt die Lösung mit dem Upwind-Schema. Es ist deutlich zu erkennen, daß sich der am Eingang schmale Übergangsbereich stromab aufgrund der überschätzten Diffusion immer stärker verbreitert. Aufgrund der vollkommenen Monotonie des Upwind-Schemas treten an keiner Stelle des Rechengebiets Oszillationen auf.
Das Bild darunter zeigt die Lösung mit QUICK. Hier ist das Profil auch
am Ausgang noch schmal, was auf hohe Genauigkeit hindeutet. Im
Außenbereich kommt es zu Oszillationen. Hier wird deutlich, daß das
hier verwendete Verfahren zur Erweiterung von einer auf zwei
Dimensionen insbesondere bei höheren Ordnungen
und unter Winkeln von
![]() kritisch wird.
kritisch wird.
Die Isolinienbilder, die auf der Basis von Lösungen mit MUSCL ermittelt wurden, weisen, wie in Abbildung 40a zu erkennen ist, keine Oszillationen auf. Die Genauigkeit ist beim nichtsymmetrischen MUSCL ein wenig besser als beim symmetrischen.
Die Ergebnisse des ENO-Schemas in Abbildung 40c und 40d weisen bei beiden Ordnungen leichte Oszillationen auf, die insbesondere in den Randbereichen auftreten. Offenbar ist gerade dieses Verfahren wegen der Verminderung der Ordnung am Rand anfällig gegenüber leichten Fehlern aufgrund von Oszillationen. Dieser Effekt ist bei der höheren Ordnung weniger stark zu beobachten. Insgesamt sind die Oszillationen hier jedoch deutlich geringer als bei dem simplen QUICK-Schema mit festem Differenzenstern.
Abschließend kann man sagen, daß es kein optimales Konvektionsschema gibt. Für die meisten turbulenten Strömungen lassen sich mit MUSCL-Schemata relativ zuverlässig gute Lösungen erzielen. In Ausnahmefällen kann man von der guten Genauigkeit eines ROE oder ENO-Schemas profitieren, wobei bei letzterem vor allem bei hoher Ordnung ein erheblich vergrößerter Rechenaufwand anfällt.
Sind die Strömungen instationär, erweist sich die TVD-Limitierung teilweise als Nachteil und das QUICK-Schema führt zu besseren Resultaten.
Da die Stabilität (Konvergenz) der Verfahren höherer Ordnung generell nicht so gut ist wie beim UDS werden Rechnungen oft mit UDS begonnen und die Diffusionskorrektur erst nach einigen Iterationen eingeschaltet.