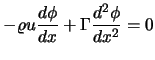 |
(5.76) |
Das prinzipielle Problem, das bei der Approximation des Konvektionsterms im Falle großer Peclet-Zahlen auftritt, kann bereits an einem sehr einfachen Testfall beobachtet werden. Auch für eine Gegenüberstellung der unterschiedlichen Approximierungsschemata ist es weitgehend ausreichend, die eindimensionale Konvektions-Diffusions-Differentialgleichung zu betrachten und die Resultate zu vergleichen.
Betrachtet werden soll eine Finite-Volumen-Approximation der
Differentialgleichung
| (5.77) |
Für die Kontrollvolumen wird ein nichtäquidistantes Gitter verwendet,
das in positiver x-Richtung verdichtet ist. Im entscheidenen Bereich bei
![]() beträgt der Gitterabstand
beträgt der Gitterabstand
![]() .
Es werden jeweils die Ergebnisse bei zwei unterschiedlichen P-Zahlen
betrachtet:
.
Es werden jeweils die Ergebnisse bei zwei unterschiedlichen P-Zahlen
betrachtet:
![]() ;
; ![]() und
und
![]() .
.
Die Problematik der nichtlimitierten Differenzenschemata ist in
Abbildung 34 zu erkennen. Die Abbildungen auf der linken
Seite zeigen Lösungen bei ![]() , also bei einer kleinen Peclet-Zahl,
in den Abbildungen rechts beträgt die Peclet-Zahl
, also bei einer kleinen Peclet-Zahl,
in den Abbildungen rechts beträgt die Peclet-Zahl ![]() .
Während sich bei der kleinen
P-Zahl mit höherer Ordnung für die Zentraldifferenzenapproximation
und QUICK immer bessere Ergebnisse zeigen, ist bei der hohen P-Zahl von
30 zu erkennen, daß die nichtlimitierten Verfahren hier zu starken
Oszillationen in der Lösung neigen. Dies gilt für QUICK, CUI,
Flux-Blending und insbesondere für das CDS-Verfahren.
.
Während sich bei der kleinen
P-Zahl mit höherer Ordnung für die Zentraldifferenzenapproximation
und QUICK immer bessere Ergebnisse zeigen, ist bei der hohen P-Zahl von
30 zu erkennen, daß die nichtlimitierten Verfahren hier zu starken
Oszillationen in der Lösung neigen. Dies gilt für QUICK, CUI,
Flux-Blending und insbesondere für das CDS-Verfahren.
Wie zu erwarten war, verhindern TVD-Verfahren Oszillationen, die bei nichtlimitierten Schemata zu beobachten sind. Es ergibt sich sowohl bei der großen als auch bei der kleinen Peclet-Zahl eine Lösung, die der exakten sehr nahe kommt, wie in Abbildung 35 zu erkennen ist.
Während bei ![]() kaum ein Unterschied zwischen den einzelnen
Verfahren zu beobachten ist, werden die Unterschiede bei
kaum ein Unterschied zwischen den einzelnen
Verfahren zu beobachten ist, werden die Unterschiede bei ![]() deutlich. Hier zeigt sich im oberen Bild, daß der Parameter
deutlich. Hier zeigt sich im oberen Bild, daß der Parameter ![]() im MUSCL-Schema offenbar kaum eine Rolle spielt - alle Kurven für
unterschiedliche Varianten fallen zusammen.
im MUSCL-Schema offenbar kaum eine Rolle spielt - alle Kurven für
unterschiedliche Varianten fallen zusammen.
In Abbildung 36 sind die Ergebnisse der eindimensionalen skalaren Transportgleichung mit Hilfe einer ENO-Lösung unterschiedlicher Ordnung dargestellt. Bei der geringen Peclet-Zahl zeigen sich die Vorteile der hohen Ordnung, ENO-Verfahren treffen die exakte Lösung sogar noch besser als beispielsweise das MUSCL-Verfahren. Bei der hohen Peclet-Zahl sind die Verhältnisse anders. Speziell dieser Fall ist für ein ENO-Verfahren problematisch, da wegen des Charakters der exakten Lösung stets ein Differenzenstern verwendet wird, der sich nach links ausrichtet. Dadurch ist dem Verfahren die Möglichikeit genommen, durch Variation der Stützpunkte Oszillationen zu vermeiden.