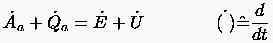
Die Diskussion unterschiedlicher zeitlicher Approximationsverfahren soll am Beispiel der Wärmeleitung erfolgen. Die Bilanzgleichung der (ebenen) Wärmeleitung leitet sich aus dem (auf thermisch-mechanische Umsetzungen beschränkten) Energiesatz
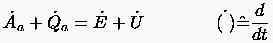
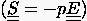 ,
inkompressiblen
,
inkompressiblen 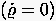 Fluids, verschwinden ähnlich wie bei einem starren Körper alle
Spannungsleistungen
Fluids, verschwinden ähnlich wie bei einem starren Körper alle
Spannungsleistungen 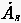 , weswegen der Arbeitsansatz der Mechanik
die Identität
, weswegen der Arbeitsansatz der Mechanik
die Identität
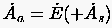
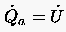 |
(3.1) |
möglich. Die in der Zeiteinheit zugeführte Wärmemenge sei ausschließlich leistungsbedingt
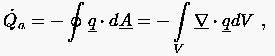
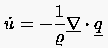 |
(3.2) |
erhalten. Berücksichtigt man den Zusammenhang
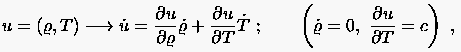
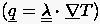 nur noch eine abhängige Variable auf,
und man erhält
nur noch eine abhängige Variable auf,
und man erhält
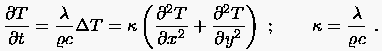 |
(3.3) |
Die partielle Differentialgleichung (3.3) ist elliptisch in Raum und parabolisch in der Zeit. Wir wenden uns nun einem einfachen Beispiel, der Temperaturverteilung in einem dünnen gleichförmigen Stab, dessen Schwerachse mit der Raumkoordinate zusammenfallen möge, zu. Zusätzlich setzen wir voraus, daß der Stab an seinem Mantel wärmeisoliert ist, also die Temperaturveränderungen durch Wärmeleitung in Längenrichtung und durch Wärmeübertragung an den Enden eintreten. Das Problem wird durch die partielle Differentialgleichung
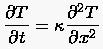 |
(3.4) |
beschrieben.