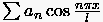 und
und
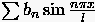 durch das äquivalente
durch das äquivalente
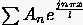 , wobei
, wobei 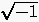 der
Definitionsbereich der Funktion ist.
der
Definitionsbereich der Funktion ist.
Die Methode drückt eine zu Beginn vorhandene Fehlerzeile durch eine endliche Fourierreihe aus und verfolgt mittels der bekannten Methode der Trennung der Variablen das Anwachsen einer Funktion, die sich für auf diese Reihe reduziert.
Die Fourierreihe kann mit Sinus- und Cosinus-Gliedern aufgebaut werden,
wird jedoch aus rechentechnischen Gründen in exponentieller
Schreibweise notiert. Man ersetzt 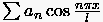 und
und
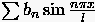 durch das äquivalente
durch das äquivalente
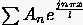 , wobei
, wobei 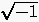 der
Definitionsbereich der Funktion ist.
der
Definitionsbereich der Funktion ist.
Wir bezeichnen die Fehler in den Gitterpunkten auf zwischen und mit . Die Gleichungen
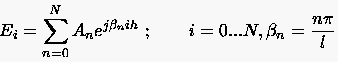 |
(3.24) |
genügen zur eindeutigen Bestimmung der unbekannten Koeffizienten
und zeigen, daß sich eine beliebige Verteilung der
Anfangsfehler in dieser komplexen Form darstellen läßt. Da die finiten
Differenzenformulierungen der zu untersuchenden PDG stets linear sein
werden, lassen sich sämtliche Lösungen (auch die Fehlerbehafteten)
überlagern. Wir betrachten daher in der Folge lediglich einen einzigen,
jedoch beliebigen Term der Reihe (3.24), um an diesem zu untersuchen,
unter welchen Voraussetzungen er zeitlich nicht wächst. Wenn wir
tatsächlich keinerlei Einschränkungen bezüglich machen, so wird
auch die Überlagerung mehrerer beliebiger Terme aus (3.24) zeitlich
beschränkt bleiben. Um die Ausbreitung dieses Fehlers mit wachsendem
zu untersuchen, müssen wir zunächst eine Lösung der endlichen
Differenzengleichung finden, die sich für 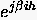 reduziert. Wir machen den Separationsansatz
reduziert. Wir machen den Separationsansatz
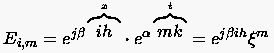 |
(3.25) |
mit der im allgemeinen Konstanten . Der Fehler wächst offensichtlich nicht mit , wenn || < 1 ist.
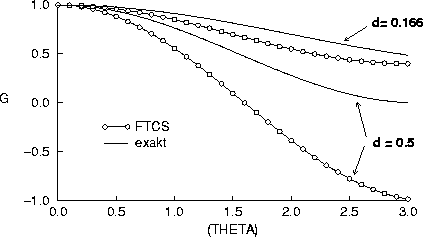
Hierzu betrachten wir erneut die FTCS Diskretisierung (3.5) der eindimensionalen Wärmeleitungsgleichung
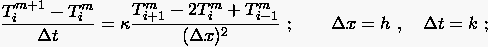
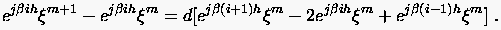
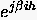 führt auf
führt auf
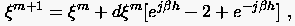
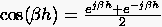 auf
auf

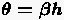 gültige Beziehung
gültige Beziehung
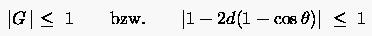

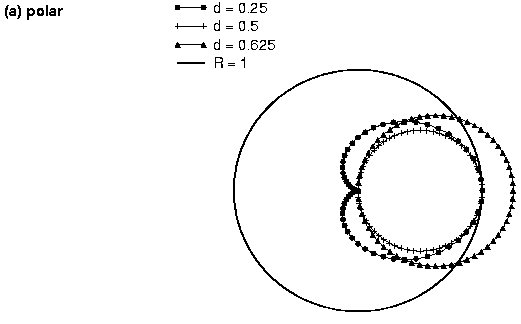 |
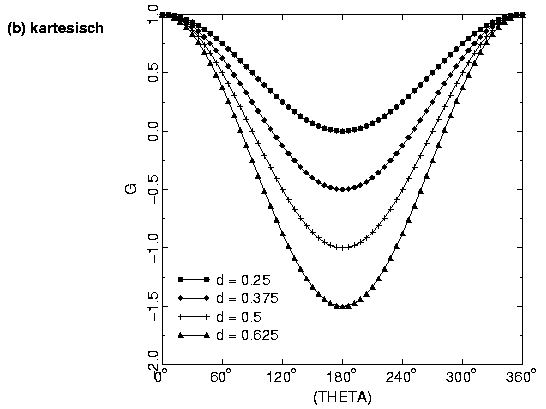 |
Für die implizite BTCS Formulierung (3.7) berechnet sich der Vergrößerungsfaktor gemäß
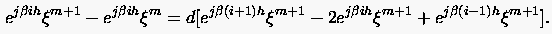
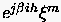 führt auf die Gleichung
führt auf die Gleichung
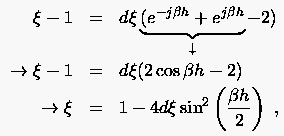
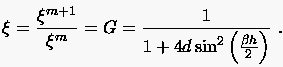
Ein weiteres Kriterium zur Beurteilung der (stabilen) Diskretisation einer partiellen Differentialgleichung ergibt sich aus dem Vergleich ihres Dämpfungsverhaltens mit dem Dämpfungsverhalten der Ausgangsgleichung. Den Abklingfaktor des kontinuierlich gestellten Problems berechnet man wie folgt:
Zunächst ist die im Separationsansatz (3.25)
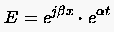
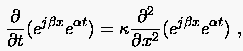
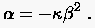
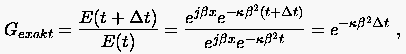 |
(3.26) |
bzw. mit 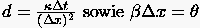 zu
zu
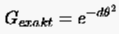
 |