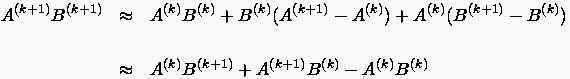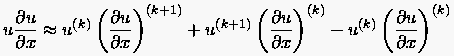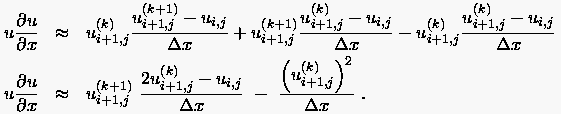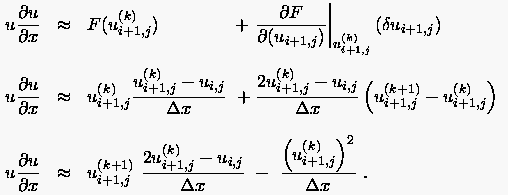Next: Anwendungsbeispiele
Up: Zeitapproximation -
parabolische Diffentialgleichungen
Previous: Zyklische oder periodische Randbedingung
Bei der Diskretisierung von Differentialgleichungen mit Hilfe
numerischer Approximationsverfahren muß beachetet werden, daß
effiziente Löser nur für lineare Gleichungssysteme zur
Verfügung stehen. Da die Diskretisierung nichtlinearer
Differentialgleichungen auch auf nichtlineare Gleichungssysteme
führt, müssen derartige Systeme linearisiert werden.
Viele Strömungsbilanzgleichungen sind nichtlinear (z.B. Konvektion).
Wir betrachten exemplarisch den Term 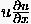 aus der Impulsbilanz für 2d-Strömungen. Die rückwärtige
FD-Approximation in positiver -Richtung führt dabei auf:
aus der Impulsbilanz für 2d-Strömungen. Die rückwärtige
FD-Approximation in positiver -Richtung führt dabei auf:
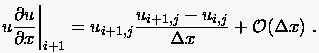 |
(3.73) |
Diese Differenzengleichung ist nichtlinear für den unbekannten
Term .
Zur Linearisierung stehen unterschiedliche Methoden zur Verfügung:
- Beim Lagging wird der Koeffizient von der bekannten
Station genommen:
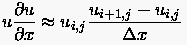
- Bei der iterativen Methode wird der zurückliegende Wert
(zeitlich bzw. iterativ) solange durch neue Lösungen
verbessert, bis ein Konvergenzkriterium erfüllt ist.
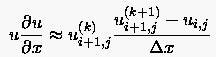
- Newton-Linearisierung des Terms mit Änderung zweier
aufeinanderfolgender Iterationen.

Für den nichtlinearen Term erhält man:
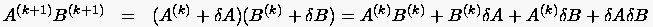
und ohne den von höherer Ordnung kleinen Term 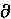 A
A 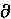 B
B
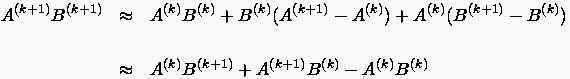
Die Anwendung auf den konvektiven Term führt auf:
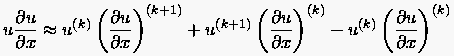
Damit lautet die Approximation:
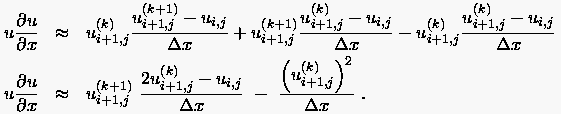
Bei der Newton Linearisierung muß der Startwert in der Nähe
der Lösung liegen. Bei parabolischen PDG ist dies durch
Fortschreiten in der parabolischen Richtung möglich.
- Bei der Linearisierung mit Hilfe einer Taylorreihe wird
ausgehend von einem bekannten Wert der Iterationsstufe
eine Reihenentwicklung durchgeführt:

Angewandt auf Gleichung (3.73) ergibt das
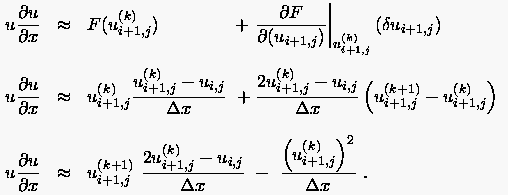




Next: Anwendungsbeispiele
Up: Zeitapproximation -
parabolische Diffentialgleichungen
Previous: Zyklische oder periodische Randbedingung
Benjamin Gilde
Sat Dec 16 15:24:45 CET 2000
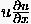 aus der Impulsbilanz für 2d-Strömungen. Die rückwärtige
FD-Approximation in positiver -Richtung führt dabei auf:
aus der Impulsbilanz für 2d-Strömungen. Die rückwärtige
FD-Approximation in positiver -Richtung führt dabei auf:
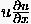 aus der Impulsbilanz für 2d-Strömungen. Die rückwärtige
FD-Approximation in positiver -Richtung führt dabei auf:
aus der Impulsbilanz für 2d-Strömungen. Die rückwärtige
FD-Approximation in positiver -Richtung führt dabei auf:
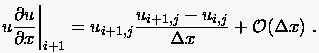
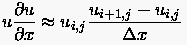
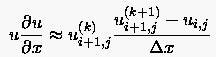

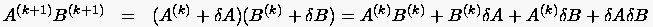
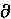 A
A 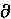 B
B