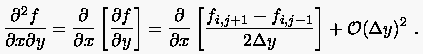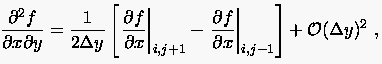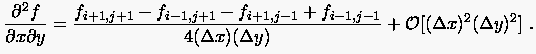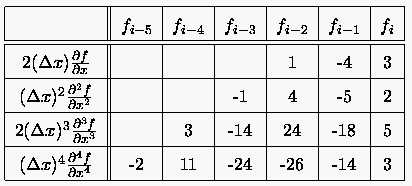Next: Zeitapproximation -
parabolische Diffentialgleichungen
Up: Finite Differenzenmethoden
Previous: Nichtäquidistante Gitter
Algebraische Näherungen für gemischte partielle Ableitungen leitet
man unmittelbar von den vorangestellten Überlegungen zu gewöhnlichen
Differentiationsprozessen ab. Eine finite Differenzenformulierung von
quadratischer Fehlerordnung für
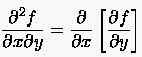
findet man etwa, indem man den Ausdruck 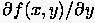 diskretisiert
diskretisiert
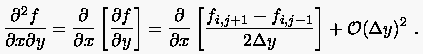
Wegen der Unabhängigkeit der Variablen formuliert man weiter
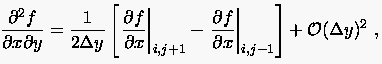
und erhält nach erneuter Verwendung zentraler Differenzenquotienten
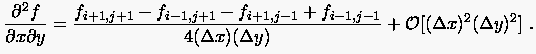 |
(2.35) |
Der Vollständigkeit halber sei erwähnt, daß man dasselbe Ergebnis
auch aus Taylorreihenentwicklungen der Funktion um das
Entwicklungszentrum errechnen kann.
Tabelle 1: Zentrale Differenzenquotienten
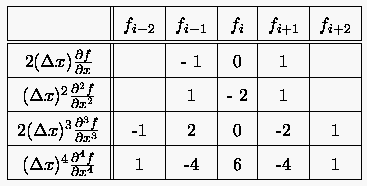 |
Tabelle 2: Vorwärtige Differenzenquotienten
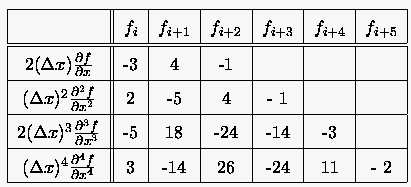 |
Tabelle 3: Rückwärtige Differenzenquotienten
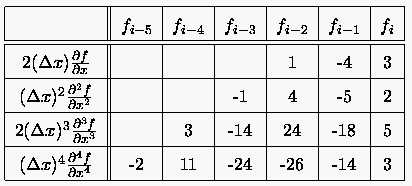 |
Tabelle 4: Zentrale Differenzenquotienten
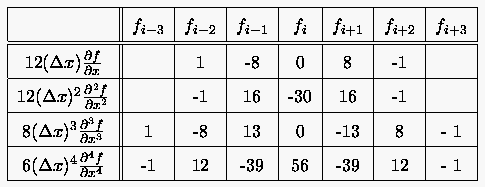 |
Tabelle 5: Vorwärtige Differenzenquotienten
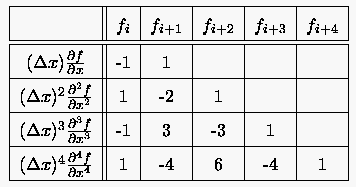 |
Tabelle 6: Rückwärtige Differenzenquotienten
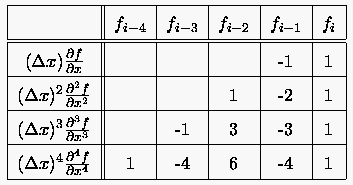 |




Next: Zeitapproximation -
parabolische Diffentialgleichungen
Up: Finite Differenzenmethoden
Previous: Nichtäquidistante Gitter
Benjamin Gilde
Sat Dec 16 15:24:45 CET 2000
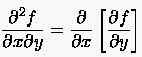
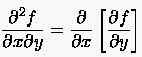
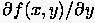 diskretisiert
diskretisiert