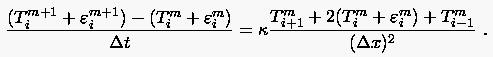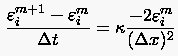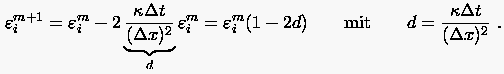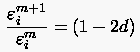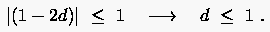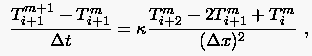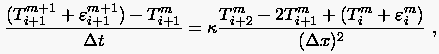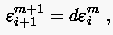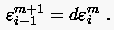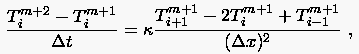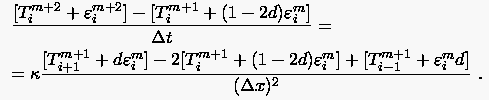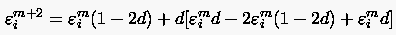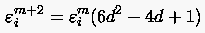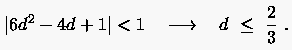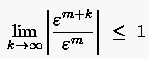Next: Matrizenkriterium
Up: Stabilität
Previous: Stabilität
Die FTCS Diskretisierung der PDG
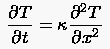
lautet
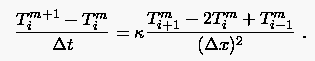 |
(3.9) |
Wir wollen nun die Auswirkung einer in () eingeleiteten Störung 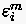 auf den Knotenpunkt () untersuchen. Hierzu
notieren wir
auf den Knotenpunkt () untersuchen. Hierzu
notieren wir
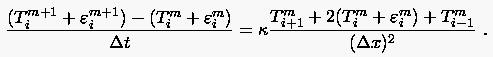 |
(3.10) |
Die Subtraktion von (3.9) und (3.10) liefert
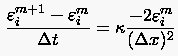
bzw.
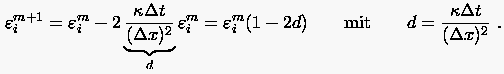
und damit
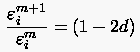
Die mathematische Formulierung der Stabilität, wonach eine relative
Vergrößerung der Störung dem Betrage nach vermieden werden muß,
lautet also
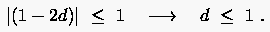 |
(3.11) |
Als nächstes wenden wir uns der im Knoten
induzierten Störung zu. Hierzu notieren wir
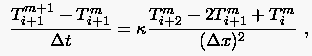 |
(3.12) |
sowie
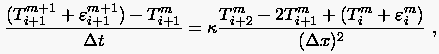 |
(3.13) |
Subtrahiert man Gleichung (3.12) von Gleichung (3.13),
dann erhält man
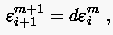
und analog für den Knoten
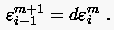
(Der Fall zeigt somit deutlich, wie sich eine Störung entlang der
charakteristischen Kurven ausbreitet.) Die letzten beiden Ergebnisse
benutzen wir, um die Induktion in dem Knoten , der zwei
Zeitschritte oberhalb der Störquelle liegt, zu erfassen.
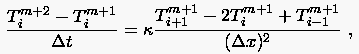 |
(3.14) |
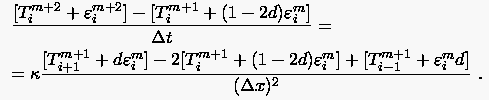 |
(3.15) |
Die stabile Lösung ermittelt man aus
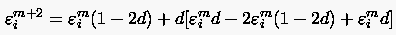
bzw.
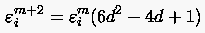
zu
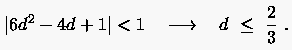 |
(3.16) |
Schreitet man zu höheren Zeitlinien fort, so ergeben sich zunehmend
restriktivere Bedingungen für . Die Abbildungen 36 und
37 veranschaulichen das Stabilitätsverhalten der FTCS
Formulierung. Für erkennt man eine oszillierende Instabilität,
die man daher auch dynamische Instabilität nennt. Wächst die Amplitude
ohne einen Vorzeichenwechsel, so nennt man dies statische Instabilität.
Wir wollen nun versuchen, den Grenzwert von , der durch
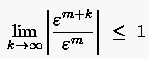
festgelegt ist, zu ermitteln. Hierzu formulieren wir im nächsten
Abschnitt ein Matrizenkriterium.
Abbildung 24: FTCS Diskretisierung von (3.4). Dämpfung einer im
Knoten aufgebrachten Störung durch hinreichend
kleines .
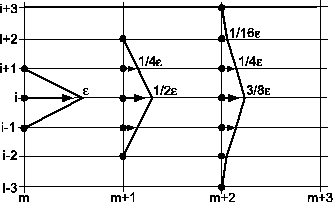 |
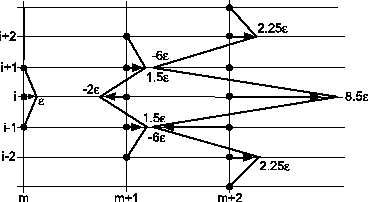
Abbildung 25: Illustration zur Fehlervergrößerung bei FTCS Diskretisierung
von (3.4) für ( dynamische Instabilität).
 |




Next: Matrizenkriterium
Up: Stabilität
Previous: Stabilität
Benjamin Gilde
Sat Dec 16 15:24:45 CET 2000
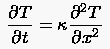
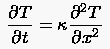
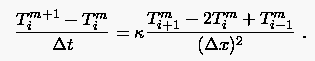
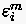 auf den Knotenpunkt () untersuchen. Hierzu
notieren wir
auf den Knotenpunkt () untersuchen. Hierzu
notieren wir