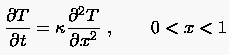
Das in der Folge beschriebene Verfahren besteht im wesentlichen darin, die finiten Differenzengleichungen durch Matrizen auszudrücken und dann die Eigenwerte einer assoziierten Matrix zu u÷ntersuchen.
Wir betrachten die Gleichung
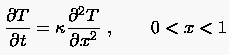
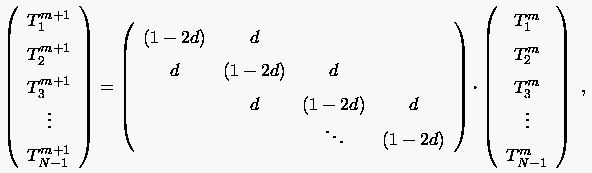
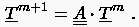 |
(3.17) |
Hiermit lassen sich die Temperaturen zu einer beliebigen Zeitlinie auf die bekannten Anfangstemperaturen zurückführen
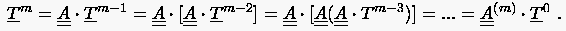
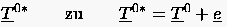
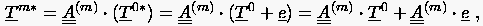
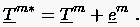
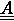 ausdrückt.
Angenommen die symmetrische Matrix
ausdrückt.
Angenommen die symmetrische Matrix 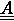 verfügt über paarweise
verschiedene Eigenwerte
verfügt über paarweise
verschiedene Eigenwerte 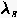 , dann sind die dazugehörigen Eigenvektoren
linear unabhängig. Der Fehlervektor ergibt sich durch
Linearkombinationen der Eigenvektoren von
, dann sind die dazugehörigen Eigenvektoren
linear unabhängig. Der Fehlervektor ergibt sich durch
Linearkombinationen der Eigenvektoren von 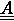 zu
zu
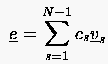 |
(3.18) |
Für den Vektor der induzierten Fehler auf einer Zeitlinie notieren wir
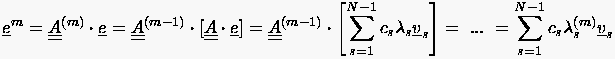 |
(3.19) |
was besagt, daß die Fehler mit nicht exponentiell anwachsen, sobald kein Eigenwert dem Betrag nach größer 1 ist.
Zunächst noch eine Bemerkung über die Eigenwerte einer gewöhnlichen tridiagonalen Matrix
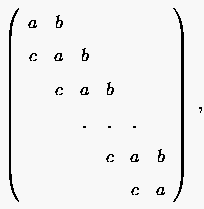
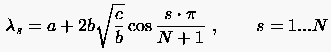 |
(3.20) |
Zerlegen wir die Matrix 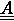 für die FTCS Formulierung aus
Gleichung (3.17) in zwei Teilmatrizen
für die FTCS Formulierung aus
Gleichung (3.17) in zwei Teilmatrizen
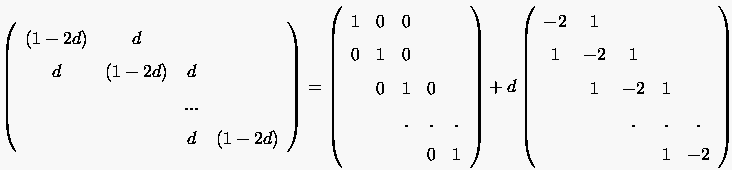
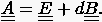 . Damit erleichtert sich
die Suche nach den Eigenwerten
. Damit erleichtert sich
die Suche nach den Eigenwerten
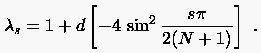 |
(3.21) |
Das explizite Verfahren ist stabil für
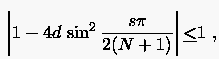
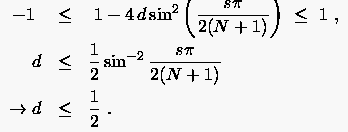 |
(3.22) |
Für die implizite BTCS Formulierung
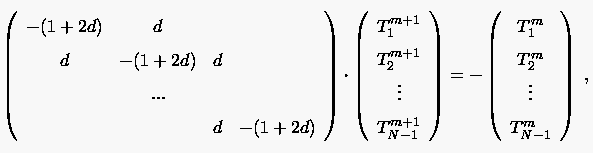
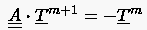
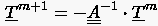
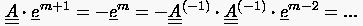
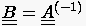
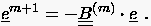
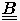 lauten
lauten
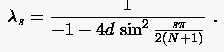 |
(3.23) |
Sie sind in jedem Falle betragsmäßig kleiner eins, weshalb das implizite Verfahren generell stabil ist.