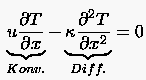
Konsistenz hat jedoch nicht immer auch Konvergenz zur Folge, denn es kann durchaus sein, daß die Lösung der Differentialgleichung das Differenzenschema erfüllt, obgleich die Lösung der finiten Approximation nicht gegen die Lösung der DGL konvergiert. Welche Kriterien erfüllt sein müssen, damit Konvergenz vorliegt, soll an einem Beispiel verdeutlicht werden. Betrachten wir die Wärmetransportgleichung mit Konvektion:
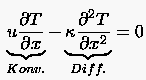 |
(3.43) |
mit den Randbedingungen
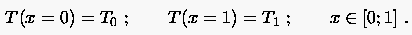
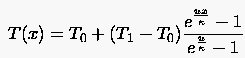 |
(3.44) |
Approximiert man die in (3.43) auftretenden Differentialquotienten auf einem äquidistanten Rechengitter durch
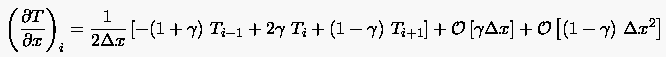 |
(3.45) |
mit dem sog. Flux-blending Faktor 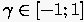 für die erste
Ableitung, bzw.
für die erste
Ableitung, bzw.
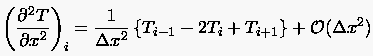
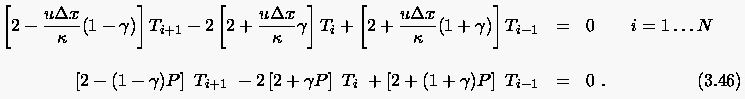 |
(3.46) |
Der auftretende Ausdruck 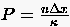 bestimmt
das lokale Verhältnis von konvektivem zu diffusivem Transport.
Man nennt ihn daher auch Peclet-Zahl oder
Zellreynoldszahl. Anhand dieser Kennzahl läßt sich beurteilen,
inwieweit die Transporteigenschaften der Ausgangs-Differentialgleichung
mit denen des Differenzenschemas übereinstimmen. Die analytische
Lösung der Differenzengleichung (3.46), bestimmt mit Hilfe des
Ansatzes , lautet
bestimmt
das lokale Verhältnis von konvektivem zu diffusivem Transport.
Man nennt ihn daher auch Peclet-Zahl oder
Zellreynoldszahl. Anhand dieser Kennzahl läßt sich beurteilen,
inwieweit die Transporteigenschaften der Ausgangs-Differentialgleichung
mit denen des Differenzenschemas übereinstimmen. Die analytische
Lösung der Differenzengleichung (3.46), bestimmt mit Hilfe des
Ansatzes , lautet
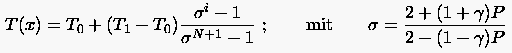 |
(3.47) |
Sollte das Differenzenschema (3.46) konsistent zur DGL (3.43) sein, so muß der Abschneidefehler für verschwindende Schrittweiten gegen Null streben. Die Bestimmung des Abschneidefehlers geschieht durch Taylorreihenentwicklung von bzw. :
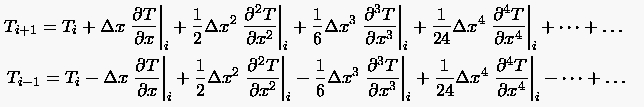
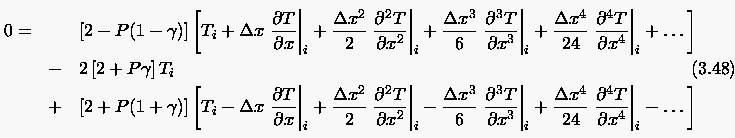 |
(3.48) |
und subtrahiert davon die zu lösende Differentialgleichung, so
erhält man den Abschneidefehler 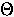
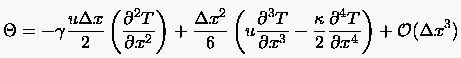 |
(3.49) |
Die Bestimmungsgleichung des Abschneidefehlers zeigt, daß das
Differenzenschema konsistent zur DGL ist. Die Konsistens ist von der
Ordnung und hat aufgrund des
damit verbundenen Gliedes 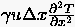 ''dissipativen'' Charakter. Verallgemeinert bezeichnet man den
Charakter eines Abschneidefehlers als ''dissipativ'', falls der
führende Summand von gerader Ordnung ist, bzw. als ''dispersiv'',
falls er von ungerader Ordnung ist. Im Falle spricht
man auch von numerischer Diffusion.
''dissipativen'' Charakter. Verallgemeinert bezeichnet man den
Charakter eines Abschneidefehlers als ''dissipativ'', falls der
führende Summand von gerader Ordnung ist, bzw. als ''dispersiv'',
falls er von ungerader Ordnung ist. Im Falle spricht
man auch von numerischer Diffusion.
Zur Konvergenzuntersuchung betrachten wir die analytische Lösung der Differenzengleichung. Für Parameterwerte erhält man positive Werte im Falle gerader Exponenten und negative Werte im Falle ungerader Exponenten. Diese Tatsache erklärt, warum es zu Oszillationen in der numerischen Lösung kommen kann, die ein divergentes Lösungsverhalten hervorrufen können. Die Differenzenformel ist dagegen konvergent, wenn der Parameter ist. Daraus folgt:
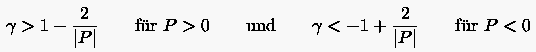 |
(3.50) |
In diesem Fall ist der Koeffizient der zentralen Stellen '''' des Schemas (3.46) dominant gegenüber denen der äußeren Stellen '''' bzw. ''''. Die konvergente Differenzenformel (3.46) führt daher auch auf eine günstige diagonaldominante Koeffizientenmatrix.
Mit Hilfe der oben angestellten Überlegungen läßt sich das sogenannte Lax-Äquivalenz-Theorem formulieren:
Das Differenzenschema einer linearen Differentialgleichung bzw. eines Anfangswertproblems ist genau dann konvergent, wenn es sowohl stabil als auch konsistent zur Differentialgleichung ist.
Für den Parameter seien zwei Spezialfälle unterschieden:
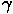 =0:
=0:
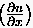 ; Konsistenz und
Konvergenzordnung , diagonaldominante
Koeffizientenmatrix für |P} < 2.
; Konsistenz und
Konvergenzordnung , diagonaldominante
Koeffizientenmatrix für |P} < 2.
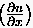 ; Konsistenz und
Konvergenzordnung , Diagonaldominanz und somit
auch Konvergenz für alle .
; Konsistenz und
Konvergenzordnung , Diagonaldominanz und somit
auch Konvergenz für alle .
Die Wahl des Parameters zu einer bekannten Peclet-Zahl gemäß (3.50) sichert die Diagonaldominanz des Gleichungssystems und stellt ein gewichtetes Mittel der beiden oben erwähnten Extremfälle dar ( ''upwinding''). Der Differenzenquotient des konvektiven Terms folgt der Strömungsrichtung. Für positive Geschwindigkeiten verwendet man demnach rückwärtige Differenzenquotienten, für negative Geschwindigkeiten vorwärtige Differenzenquotienten zur Approximation der partiellen Ableitungen. Durch den konvektiven Anteil der DGL (3.43) wird eine Impulsgröße oder Störung lediglich stromab, d.h. entlang der Bahnlinien transportiert. Diese nichtsymmetrische Eigenschaft sollte bei der finiten Approximation möglichst erhalten bleiben. Sie ist bei der Verwendung zentraler Differenzen nicht erfüllt und führte einerseits zur Entwicklung sog. Lagrange-Verfahren, bei denen der konvektive Term (physikalisch richtig) entlang der Bahnlinien integriert wird, sowie andererseits zu einer ganzen Reihe von richtungsabhängigen Upwind-Strategien.
Das Hauptproblem bei der Diskretisation von (Eulerschen-) Transportgleichungen besteht in der Approximation der konvektiven Terme, da diese häufig nichtlinear sind und ihre Differentialoperatoren keine Symmetrieeigenschaften besitzen. Im Falle stark konvektionsbehafteter Probleme () ist ein ''Upwinding'' häufig unausweichlich. Bei Verwendung von Zentraldifferenzen würde das Integrationsgebiet dann in zwei voneinander nahezu unabhängige Bereiche zerfallen. Diese sind aufgrund des Verlusts der Hauptdiagonalwerte in der Koeffizientenmatrix schachbrettartig zueinander angeordnet. Der exakten Lösung des Differenzenschemas können dann beliebige alternierende Wertefolgen überlagert werden, die das Differenzenschema ebenfalls erfüllen.
Der Nachteil einer Upwind-Diskretisation liegt in der verringerten Genauigkeit der Approximation. Sie erzeugt aufgrund der Zusammensetzung des führenden Fehlergliedes numerische Diffusion. Für stark konvektionsbehaftete Probleme dominiert dann nicht nur der konvektive Term sondern auch der führende Fehler der Approximation den Diffusionsterm des Problems. Die diffusiven Transporteigenschaften der Differentialgleichung werden durch die numerische Diffusion der Approximation überlagert.