Modifizierte Gleichungen

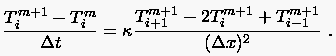
Bislang haben wir den Diskretisierungsfehler einer endlichen Differenzenformel nur der Größenordnung nach angegeben. Ziel dieses Abschnittes ist die Präzisierung von Diskretisierungsfehlern nach einer von Warming und Hyett 1974 vorgestellten Methode. Wir werden uns wieder auf die FTCS und BTCS Formulierung der eindimensionalen instationären Wärmeleitungsgleichung stützen. Eine analoge Betrachtung anderer Probleme ist leicht. Der grundlegende Gedanke zur Entwicklung der modifizierten Gleichungen ist die Rückführung der FDG in eine partielle Differentialgleichungsformulierung. Hierzu betrachten wir exemplarisch die bekannte BTCS Formulierung

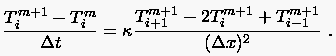
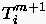Entwickelt man ausgehend vom Punkt die Ausdrücke 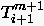und 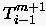in einer Taylorreihe nach der Raumkoordinate $x$

sowie $Tm$_i nach der Zeitkoordinate $t$

dann erhält man anstelle der FDG

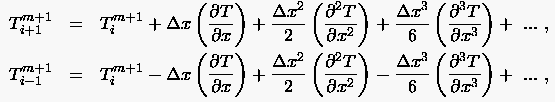
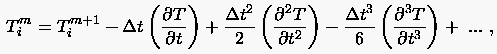
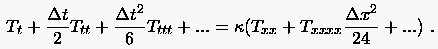(3.27)

In der Gestalt

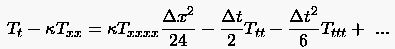(3.28)

lassen sich die Glieder der rechten Seite als Abschneidefehler der FDG interpretieren. Wir versuchen nun den Abschneidefehler in Abhängigkeit von partiellen Ableitungen in einer Variablen auszudrücken. Nochmaliges Ableiten von (3.28) nach $t$ bzw. $x2$ führt auf

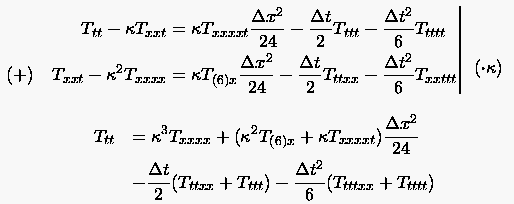(3.30)

kurz

analog durch Hinzufügen einer weiteren Zeitabteilung

Durch Einsetzen ergibt sich schließlich die äquivalente modifizierte Gleichung:

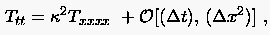
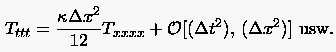
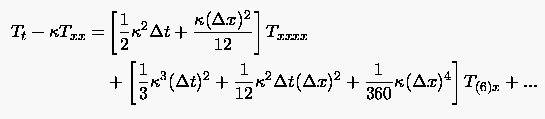(3.31)

Die zugegebenermaßen mühselige Rechnung erscheint kaum lohnenswert. Gleichung (3.31) ist zwar präziser in Hinblick auf den Diskretisationsfehler, jedoch sehr unübersichtlich. Konkrete Verbesserungen der Approximationseigenschaften ergeben sich jedoch aus der modifizierten Gleichung der FTCS Formulierung

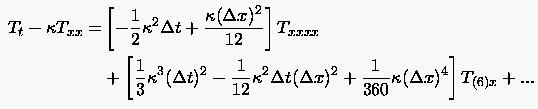(3.32)

Für die Diffusionszahl 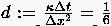verschwindet der Koeffizient der 4. Ableitung, woraus man einen Abbruchfehler $O[($x²) , (t² )] ableitet.