Next: LU-Zerlegung von tridiagonalen Matrizen Up: No Title Previous: Fehleranalyse

Behandlung linearer Gleichungssysteme

In diesem Kapitel befassen wir uns mit der Aufgabe, die linearen Gleichungssysteme, welche man aus der diskretisierten Differentialgleichung erhält, unter Berücksichtigung ihrer speziellen Struktur möglichst effizient zu lösen. Diese Gleichungssysteme haben besondere Eigenschaften: Die Koeffizientenmatrizen sind meist sehr groß, aber einfach strukturiert. Sie sind `schwach besetzt', die von Null verschiedenen Elemente treten in regelmäßiger `bandartiger' Weise in bestimmten charakteristischen Größenverhältnissen auf. Um einen ersten Eindruck zu vermitteln, wollen wir im folgenden zunächst den Prototyp einer elliptischen Differentialgleichung 2. Ordnung, die sogenannte Poissongleichung betrachten.

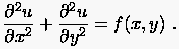(5.1)

Der Einfachheit halber beschränken wir uns auf ein quadratisches Integrationsgebiet $S$ und Dirichletsche Randbedingungen. Gesucht ist die Lösung $u(x,y)$ , welche im Gebiet $S$ die PDG $(C-1)$ erfüllt und auf dem Gebietsrand $C$ die vorgegebenen Werte

$u = g(x,y)$

annimmt. Zur Diskretisierung der Randwertaufgabe legen wir ein quadratisches Rechengitter der Schrittweite

h

zugrunde. Die Anzahl

N

der Unbekannten verhält sich dann wie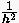

, was bei einer Unterteilung von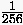

ca.

N = 65.000

Unbekannte ergibt. Die Gestalt der Koeffizienten-Matrix hängt von dem gewählten Differenzenquotienten für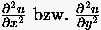

ab. Wählt man zur Approximation der zweiten partiellen Ableitung jeweils den zentralen Differenzenquotienten (2.12), so ergibt sich das folgende Gleichungssystem

$u$ _i-1,j + u_i+1,j + u_i,j-1 + u_i,j+1 - 4u_i,j = h² f_i,j
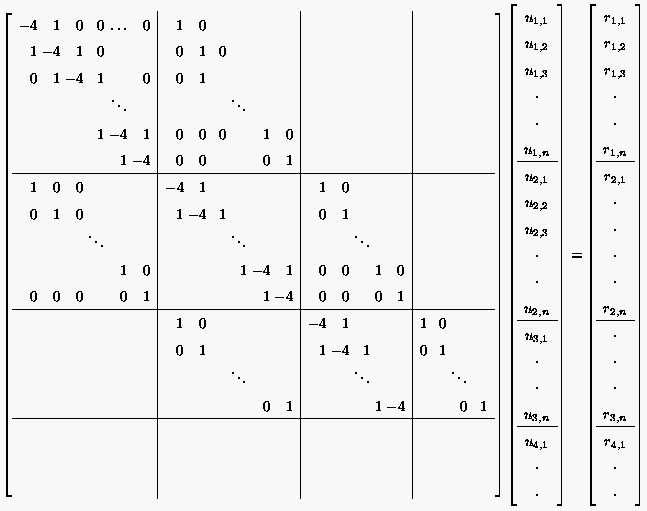
(5.2)

oder mit $h$ ² f_i,j = r_i,j auf der rechten Seite das System, das im folgenden abgedruckt ist.

Auf dieses Gleichungssystem läßt sich jedes Verfahren zur Lösung linearer Probleme anwenden. Die Effizienzunterschiede sind jedoch beträchtlich. So führt z.B. die Cramersche Regel auf ein $10$ ^204.000 Jahre währendes Geduldspiel, wohingegen moderne Verfahren bereits nach ca. 8 Sekunden zu einer Lösung gelangen. Entscheidend für die Effizienz eines Verfahrens ist der zu bewältigende Rechenaufwand, also die Anzahl der arithmetischen Operationen zur Bestimmung der Lösung. Einen ersten vergleichenden Überblick kann man sich anhand der Tabelle 7 verschaffen, die sich auf das oben skizzierte Problem bezieht.

Grundsätzlich wird zwischen direkten Lösungsmethoden, welche auf der sukzessiven Elimination der Unbekannten basieren, und iterativen Prozessen, die die gesuchte Lösung als Folge von Näherungen bestimmen, unterschieden. Der bekannteste Vertreter, der hier nicht näher diskutierten direkten Methode, ist das herkömmliche Gaußsche Eliminationsverfahren. Daneben seien das Cholesky-Verfahren zur Dreieckszerlegung symmetrisch positiver Bandmatrizen, der Thomas-Algorithmus usw. in Erinnerung gerufen.

Verfahren asymptotischer ungefähre Rechenzeit

Rechenaufwand

Gauß-Verfahren für Bandmatrizen $&quad;$ $- N$ ² ca. 20.000 sec (geschätzt)

Gauß-Seidel^*) $&quad;$ $- N$ ² ca. 10.000 sec (geschätzt)

SOR^*) $&quad;$ $- N$ ^1,5 ca. 1.200 sec

ADI^*) $&quad;$ $- N log N$ ca. 130 sec

Mehrgitterverfahren $&quad;$ $- N$ ca. 8 sec

Tabelle 7: Rechenzeiten für die diskretisierte Poisson-Gleichung im Einheitsquadrat ( $1/h = 1/256$ ), das heißt, $N = 255$ ² = 65025 Unbekannte); für die iterativen Verfahren^*) wurde eine feste relative Genauigkeit von $- 10$ ⁴ zugrunde gelegt.

**Tabelle 7:** Rechenzeiten für die diskretisierte Poisson-Gleichung im Einheitsquadrat ( $1/h = 1/256$ ), das heißt, $N = 255$ ² = 65025 Unbekannte); für die iterativen Verfahren^*) wurde eine feste relative Genauigkeit von $- 10$ ⁴ zugrunde gelegt.
Verfahren	asymptotischer	ungefähre Rechenzeit
	Rechenaufwand
Gauß-Verfahren für Bandmatrizen	$&quad;$ $- N$ ²	ca. 20.000 sec (geschätzt)
Gauß-Seidel^*)	$&quad;$ $- N$ ²	ca. 10.000 sec (geschätzt)
SOR^*)	$&quad;$ $- N$ ^1,5	ca. 1.200 sec
ADI^*)	$&quad;$ $- N log N$	ca. 130 sec
Mehrgitterverfahren	$&quad;$ $- N$	ca. 8 sec

Die direkten Lösungsmethoden erfordern die Speicherung der gesamten Koeffizientenmatrix, wodurch es leicht zur Erschöpfung des zur Verfügung stehenden Arbeitsspeichervolumens kommen kann. Die Rechenzeit wird in der Folge zu einem nicht unerheblichen Teil für die Datenkommunikation mit Hilfsspeichermedien verbraucht, weshalb sich die Lösung vor allem bei niedriger Übertragungsgeschwindigkeit erheblich verzögern kann. Mittlerweile existieren jedoch Algorithmen, die solchen Nachteilen durch sukzessive Zusammensetzung der linearen Gleichungssysteme in Verbindung mit gleichzeitiger Elimination begegnen (sog. Frontlösungsmethoden). Daneben zeichnen sich die direkten Verfahren durch die unangenehme Eigenschaft aus, die numerischen Störungen der exakten Lösung (z.B. Rundungsfehler) zu akkumulieren. Den entscheidenden Parameter zur Bestimmung der Empfindlichkeit gegenüber Störungen stellt die Konditionszahl einer Matrix (also das Produkt 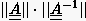nach beliebiger Norm) dar, für die man folgende `Faustregel' findet:

`Wird ein lineares Gleichungssystem mit $n$ -stelliger dezimaler Gleitkommarechnung gelöst, und beträgt die Konditionszahl der Koeffizientenmatrix = ca. 10^m, so sind aufgrund der im allgemeinen unvermeidlichen Eingangsfehler nur $(n - m -1)$ Dezimalstellen der auf die betragsmäßig größte Komponente bezogene Lösung sicher.'

Zur Senkung der Konditionszahl verfügt die Numerik über möglicherweise Abhilfe verschaffende Methoden, wie Equilibrieren, Pivotisieren, Vorkonditionieren, usw.

Im allgemeinen sind direkte Methoden wirkungsvoller als iterative Methoden, sobald

a): die Koeffizentenmatrix für eine schnelle Abschätzung des optimalen Relaxationsfaktors zu umfangreich ist;
b): die Matrix fast singulär ist, so daß kleine Reste keine kleinen Fehler in die Lösung implizieren, wie später in diesem Kapitel gezeigt wird;
c): verschiedene Gleichungssysteme mit denselben Koeffizienten, aber mit verschiedenen rechten Seiten gelöst werden müssen.

Next: LU-Zerlegung von tridiagonalen Matrizen Up: No Title Previous: Fehleranalyse

Benjamin Gilde
Sat Dec 16 15:24:45 CET 2000