Taylorreihenentwicklung

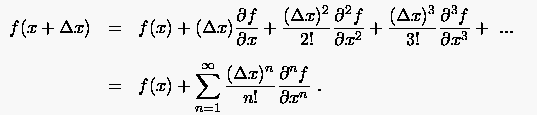
Für eine analytische Funktion $f(x)$ läßt sich der Funktionswert an einer zu $x$ benachbarten Stelle $(x\; +$x) in einer Taylorreihe entwickeln:

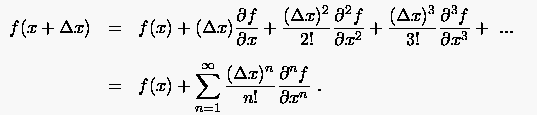(2.3)

Löst man (2.3) nach 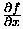auf, so erhält man

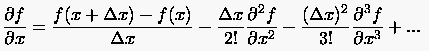(2.4)

Bricht man die rechte Seite der Glg. (2.4) nach dem ersten Glied ab und drückt den Abschneidefehler durch den für $$x < 1 führenden Fehlerterm aus, so erhält man

Eine erste finite Differenzenformulierung der ersten Ableitung ergibt sich somit aus dem bekannten vorwärtigen Differenzenquotienten

(2.5)

 

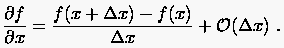
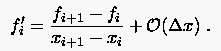Abbildung 17: Veranschaulichung der Gleichung 2.5.

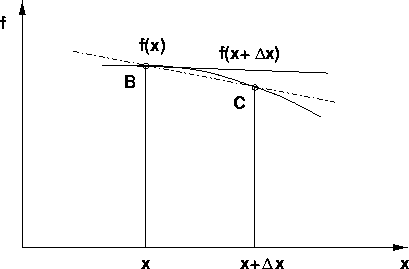Die rückwärtige Entwicklung der Funktion $f$ ergibt analog aus der Entwicklung

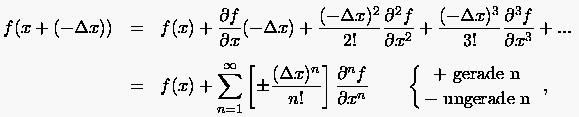(2.6)

den sogenannten rückwärtigen Differenzenquotient

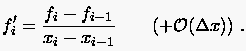(2.7)

Subtrahiert man Glg. (2.6) von Glg. (2.3), dann verschwinden für gleiche Schrittweiten alle Terme mit geraden Exponenten, und man erhält eine genauere Näherung der ersten Ableitung in Gestalt des zentralen Differenzenquotienten (2.8)

(2.8)

 

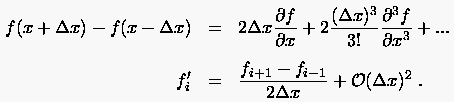Abbildung 18: Veranschaulichung der Gleichung 2.8.

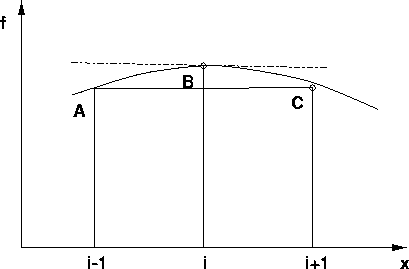Für die zweiten partiellen Ableitungen lassen sich die algebraischen Näherungen ebenfalls aus der Linearkombination verschiedenartiger Taylorreihenentwicklungen finden. Eine finite Differenzenformulierung der zweiten Ableitung findet man beispielsweise aus

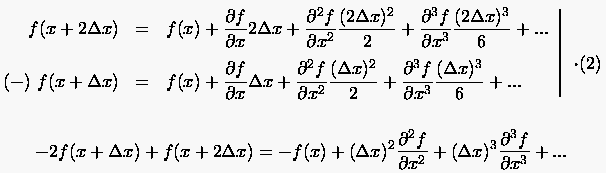(2.9)

Löst man Glg. (2.9) nach 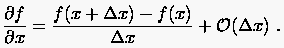auf, so erhält man den vorwärtigen Differenzenquotienten für zweite Ableitungen (2.10)

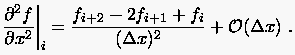(2.10)

Analog erhält man aus den rückwärtigen Entwicklungen 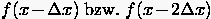den rückwärtigen Differenzenquotienten für zweite Ableitungen (2.11)

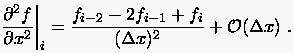(2.11)

und durch Zusammenziehen von (2.3) und (2.6) den entsprechenden zentralen Differenzenquotienten (2.12)

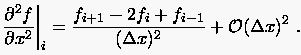(2.12)

Näherungen für höhere Ableitungen werden in gleicher Weise formuliert. Die grundlegenden Operationen der finiten Differenzenformulierung lassen sich ein wenig schematisieren, wenn man folgende Abkürzungen einführt:

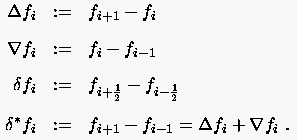(2.13)

Bekanntermaßen lassen sich lineare Differentialgleichungen, die höhere Ableitungen in einer Veränderlichen enthalten, auf ein Differentialgleichungssystem reduzieren, in dem nur noch erste Ableitungen auftreten. Die Anzahl der Gleichungen in diesem System entspricht der Ordnung der Ausgangsdifferentialgleichung. Diskretisiert man in solch einem System von $n-1$ Differentialgleichungen 1. Ordnung alle Ableitungen einheitlich (vorwärts, rückwärts oder zentral), so ergibt sich für die $n-te$ Ableitung der Funktion

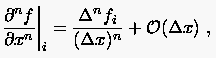(2.14)

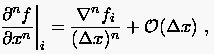(2.15)

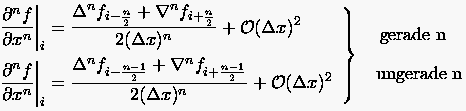(2.16)

Die hierin auftretenden $n$-ten Potenzen der Operatoren $$, $$ berechnet man zurückkehrend bis auf bekannte Werte ($$ ``rekursiv'') durch

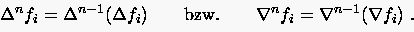(2.17)