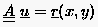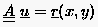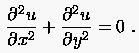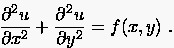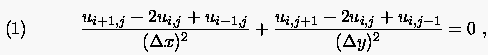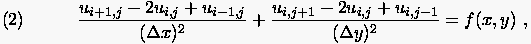Iterative Methoden

Iterative Methoden zur Lösung von algebraischen Gleichungssystemen werden im allgemeinen angewandt, wenn die Anzahl der Unbekannten groß ist, jede Gleichung aber nur einige wenige davon enthält. Die Koeffizientenmatrix besteht dann hauptsächlich aus Nullen. Die Iterationsverfahren besitzen die Eigenschaft, daß sie die schwache Besetzung der Koeffizientenmatrix voll ausnützen können und die Matrix unverändert lassen. Dies erlaubt eine bedeutend konzentriertere Speicherung der von Null verschiedenen Matrixelemente, so daß der dazu benötigte Speicherbedarf im Vergleich zu den Eliminationsmethoden bedeutend geringer ist. Bei jeder iterativen Methode beginnt man mit einem bekannten und oft beliebigen Anfangsvektor $$u⁽⁰⁾. Auf diesem aufbauend berechnet man eine Folge von Approximationen $$u^(k), die mit wachsender Iterationszahl gegen die exakte Lösung des diskretisierten Gleichungssystems (38)

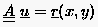
konvergieren. Wenn jede Komponente $u$_i^(k) eines Lösungsvektors $$u^(k) aus vorhandenen Schätzungen anderer Komponenten explizit berechnet wird, bezeichnet man die Prozedur als Punktmethode. Demgegenüber nennt man Prozeduren, bei denen ganze Komponentengruppen $u$_i^(k), $u$_j^(k), ... in impliziter Manier gleichzeitig berechnet werden, Linien- oder Blockmethoden. Die Teilsysteme zur Bestimmung einer Komponentengruppe löst man gewöhnlich direkt, sie können jedoch ihrerseits auch wieder iterativ gelöst werden. Den Terminus `Linienmethode' verwendet man, wenn die Elemente einer Gruppe sich zu einer kompletten Gitterlinie im Integrationsgebiet aufreihen. Ein Iterationsverfahren wird als stationär bezeichnet, wenn die Lösungsvektoren $$u^(k) aus bekannten Approximationen für alle Iterationsstufen $n$ mit dem gleichen Operationszyklus berechnet werden.

Die iterativen Verfahren wollen wir an leicht unterschiedlichen Modellgleichungen erläutern:

(1) Die Laplacegleichung

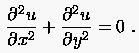(5.3)

(2) Die Poissongleichung

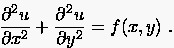(5.4)

Wir beschränken uns wiederum auf Dirichletsche Randbedingungen in einem kartesischen Rechengebiet, wollen jedoch verschieden große Schrittweiten $$x und $$y zulassen. Die finite Differenzenformulierung der beiden Modellgleichungen ergibt sich mit zentralen Differenzenquotienten zu

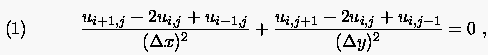(5.5)

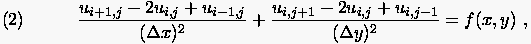(5.6)

bzw. mit $$ =

(5.7)

(5.8)

 

Abbildung 38: Veranschaulichung der 5-Punkte-Formel (44).

Verwendet man dagegen zur Näherung der zweiten partiellen Ableitung eine 9-Punkte-Formel von 4. Genauigkeitsordnung (Tabelle 4), so erhält man anstelle (44) die Beziehung

(5.9)

und somit

(5.10)

Abbildung 39: Veranschaulichung der 9-Punkte-Formel (5.9).

Abbildung 40: Skizze eines 6x6-Punkte-Rechengitters. 

Hieraus ergibt sich eine Koeffizientenmatrix von viel größerer Bandbreite und somit auch ein gesteigerter Rechenzeitbedarf. Wendet man die einfachere 5-Punkteformel (5.8) auf das in Abbildung 5.27 skizzierte 6x6-Punkte-Rechengitter mit den Randbedingungen

an, so ergibt sich für die inneren Gitterpunkte das folgende Gleichungssystem

(5.11)

bzw. mit

(5.12)

 
• Die Jacobische Iterationsmethode
• Punkt-Gauß-Seidel-Verfahren
• Konvergenzbedingung
• Linien-Gauß-Seidel Verfahren
• Sukzessive Relaxationsverfahren
• Die implizite Methode der alternierenden Richtungen
• Konvergenzkriterium
• Analytische Betrachtung der systematischen Iterationsmethoden
• Bemerkungen zum Konditionsproblem