Es ist seit langem bekannt, daß bestimmte iterative Verfahren (zum Beispiel das oben besprochene Gauß-Seidel-Verfahren) bei elliptischen Randwertaufgaben eine ''fehlerglättende'' Wirkung haben. Wir benutzen für solche Verfahren im folgenden den im Mehrgitterkontext gebräuchlichen Ausdruck Relaxationsverfahren.
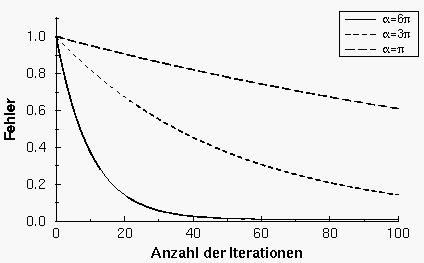
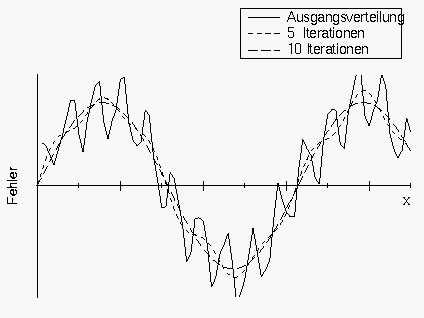
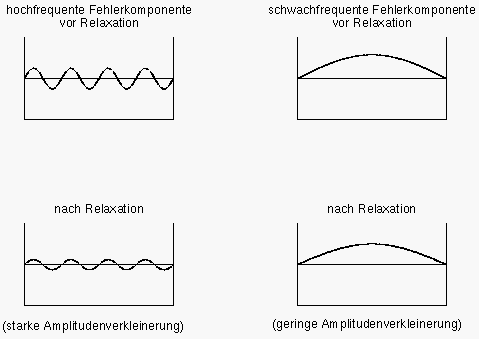
Das Gauß-Seidel-Verfahren vermag z.B. die hochfrequenten Schwingungen bei der Lösung der Laplacegleichung mit jedem Iterationsschritt um einen Faktor 0.5 zu reduzieren. Langwellige Schwingungen werden dagegen, was wir in diesem Abschnitt zeigen wollen, um einen Faktor reduziert - bei kleinem also extrem langsam. Anhand von Abbildung 46 verdeutlicht sich die ''glättende'' Wirkung dieser Verfahren. Bereits nach wenigen Iterationen besteht der Fehler hauptsächlich aus niederfrequenten Anteilen. Man hat also insgesamt keine gute Fehlerverkleinerung - und daher langsame Konvergenz - aber sehr gute Fehlerglättung (Abbildung 47). Das Konvergenzverhalten iterativer Gleichungslöser muß daher genaugenommen in Abhängigkeit von der Fehlerfreqenz beurteilt werden.
 |
 |
Auf einem groben numerischen Gitter '''' der Maschenweite kann eine finite Differenzenapproximation mit sehr viel weniger Rechenaufwand gelöst werden, als auf einem feinen, knotenpunktärmeren Gitter '''' der Maschenweite . Allerdings ergibt sich auf dem groben -Gitter im allgemeinen auch eine geringere Genauigkeit. Die Approximation einer -diskretisierten Aufgabe durch eine -diskretisierte ist daher mit einem deutlichen Informationsverlust verbunden. Hochfrequente Komponenten der Fourierreihenentwicklung vermag das grobe Gitter nicht mehr aufzulösen. Die niederfrequenten Komponenten lassen sich dagegen auf dem -Gitter gut erfassen. Hat man durch die vorangegangene Relaxation auf einem feinen Gitter eine Fehlerglättung erreicht, dann setzt sich der Fehler auf diesem Gitter im wesentlichen aus niederfrequenten Anteilen zusammen. Die Approximation des -diskretisierten Problems durch ein -diskretisiertes ist somit nun ohne wesentlichen Informationsverlust möglich. Im einfachsten Falle handelt sich um ein iteratives Verfahren, das auf einer Sequenz von mehreren Gittern abläuft. Auf jedem Gitter wird relaxiert, um die dort hochfrequenten Fehlerkomponenten zu verkleinern. Die Verbindung zwischen den verschiedenen Gittern wird durch ''Interpolations-'' und ''Restriktionsoperatoren'' hergestellt.
Die voranstehenden Aussagen über die glättende Wirkung eines Relaxationsverfahren wollen wir in einem kurzen Beispiel herleiten. Betrachtet wird dazu die PDG
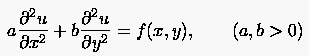
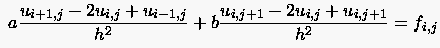 |
(5.73) |
Verwenden wir zur Glättung das Punkt-Gauß-Seidel-Verfahren, so ergibt sich für den -ten Relaxationsschritt:
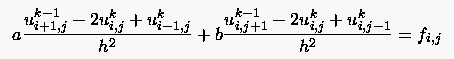 |
(5.74) |
Subtrahiert man (5.74) von (5.73) dann erhält man
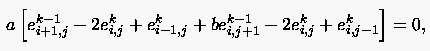 |
(5.75) |
wobei mit der lokale Fehler zwischen der jeweiligen Näherung und der diskreten Lösung gemeint ist. Wir definieren die Relation der Fehlerverstärkung
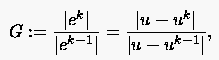
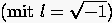
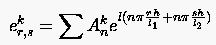
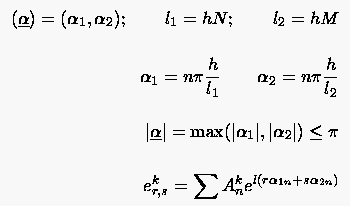 |
(5.76) |
Führt man (5.76) in (5.75) ein, so erhält man nur ein Summenglied (siehe auch Abschnitt 3.3)
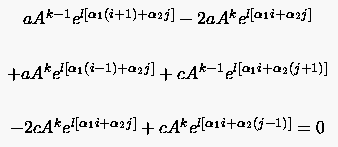 |
(5.77) |
bzw.
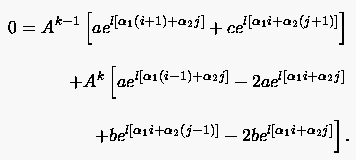 |
(5.78) |
Kürzt man nun noch den Ausdruck 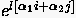 , dann erhält man für den Fehlervergrößerungsfaktor
, dann erhält man für den Fehlervergrößerungsfaktor
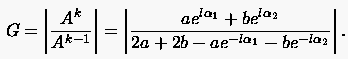 |
(5.79) |
Unter Verwendung der Eulerbeziehung 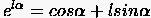 besser abschätzen:
besser abschätzen:
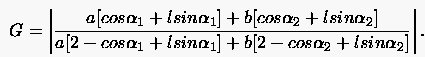 |
(5.80) |
Man beachte, daß für , gegen strebt, in diesem Falle also keine Konvergenz mehr vorliegt. Die erste nicht triviale Kombination liegt für vor. Beschränken wir uns der Einfachheit halber auf ein Integrationsgebiet vom Durchmesser , dann sind bzw. im ersten nicht trivialen Fall von gleicher Größenordnung.
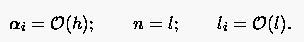
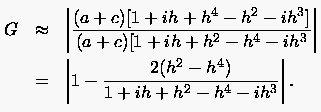 |
(5.81) |
Schätzt man den verbliebenen Nenner gegen eins ab, so ergibt sich tatsächlich für den niederfrequenten Fehler die auf einem feinen Gitter äußerst ungünstige Glättungsrate
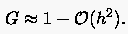
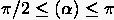 zugeordnet ist. Dies sind gerade diejenigen Frequenzen,
welche auf den nächstgröberen Gitter der Schrittweite nicht
mehr approximiert werden können und demzufolge auf
geglättet werden müssen.
zugeordnet ist. Dies sind gerade diejenigen Frequenzen,
welche auf den nächstgröberen Gitter der Schrittweite nicht
mehr approximiert werden können und demzufolge auf
geglättet werden müssen.
 |