Mehrgitterprinzip

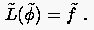
Betrachten wir eine beliebige Gleichung, fortan bezeichnet mit

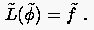(5.82)

Dabei stellt 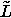einen Operator dar, der alle funktionalen Zusammenhänge der Unbekannten $$ repräsentiert und 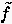die von $$ unabhangige rechte Seite der Gleichung. Eine finite Approximation der Gleichung für sämtliche diskretisierten Punkte führt zu einem Gleichssystem

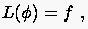(5.83)

das normalerweise iterativ gelöst wird. Bei einer linearen Gleichung ist $L$ von $$ unabhängig. Man erhält nach einigen Iterationszyklen eine Näherungslösung $$, für die die Gleichung bis auf ein Residuum $R$ erfüllt ist:

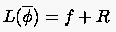(5.84)

Zur Verbesserung der Lösung muß $$ um eine Korrektur $$ ergänzt werden, mit der die Gleichung exakt erfüllt wird:

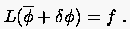(5.85)

Die Bestimmungsgleichung für die Korrektur $$ erhält man durch Subtraktion dieser beiden Gleichungen:

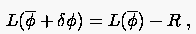(5.86)

wobei sich die Bestimmungsgleichung für $$ vereinfacht, wenn $L$ ein linearer Operator ist:

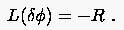(5.87)

Das Grundelement eines Mehrgitterverfahrens ist das sogenannte Zweigitterbeschleunigungsverfahren. Dabei wird nach einigen Feingitteriterationen die Korrektur $$ auf einem Grobgitter, dessen Maschenweite gegenüber dem Feingitter verdoppelt wird, bestimmt. Der niederfrequente Fehleranteil kann dadurch schneller reduziert werden. Danach erfolgen einige Nachiterationen auf dem Feingitter.