Sukzessive Relaxationsverfahren

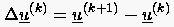
Diese Verfahren werden durch Iterationsprozesse motiviert, bei denen sich eine stetige (monotone) Entwicklung der berechneten Werte einstellt. In solchen Fällen ist man versucht, der Korrektur der Lösung zwischen zwei Iterationsschritten

einen größeren Einfluß zuzumessen, um so den Iterationsprozeß zu beschleunigen (Abbildung 5.28 unten). Aber auch der umgekehrte Ansatz, den Einfluß der Korrektur $$u^(k) bei der Bestimmung der nächstfolgenden Lösung zu dämpfen, ist denkbar, etwa wenn der Iterationsprozeß zu starken Schwingungen neigt (Abbildung 5.28 oben). Eine sehr simple verallgemeinerte Rechenvorschrift erhält man, in dem die Korrektur der $k$-ten Lösung mit einem konstanten Relaxationsfaktor < 0 multipliziert und zur rückwärtigen Lösung $$u^(k) addiert wird.

 

Abbildung 43: Unterschiedlicher Verlauf der Iteration bzw. der zeitlichen Lösung

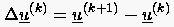
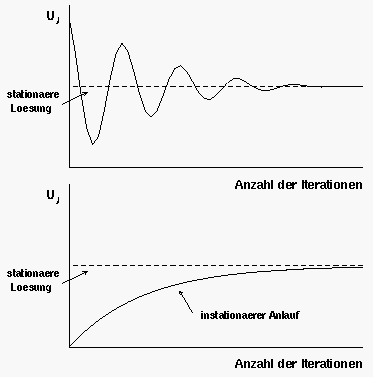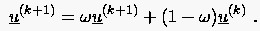(5.24)

Konkret ergibt sich anstelle von (5.20) die sukzessive Relaxationsvorschrift für das Punkt-Gauß-Seidel-Verfahren

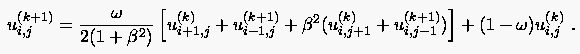(5.25)

bzw. anstelle von (5.23) die entsprechende Formulierung der Linienmethode

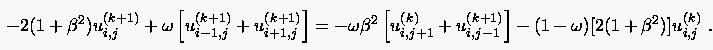(5.26)

In Abhängigkeit vom Relaxationsfaktor $$ spricht man von

• Überrelaxation falls < 2,
• Unterrelaxation falls < 1.

Der Fall $$= 1 führt wieder auf die Beziehungen (5.20) bzw. (5.23).

Die Schwierigkeit bei der Anwendung sukzessiver Relaxationsverfahren besteht in der Vorhersage optimaler Relaxationsfaktoren. Gewöhnlich sind zur Bestimmung von $$ numerische Experimente notwendig, lediglich in Ausnahmefällen findet man Empfehlungen zur Wahl des optimalen Faktors. Ein solcher Fall liegt bei der Lösung einer Laplace-DGL in einem rechteckigen Gebiet mit Dirichletschen Randbedingungen vor. Diskretisiert man das Problem auf ein Gitter mit konstanten Schrittweiten, so gilt

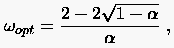(5.27)

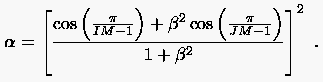(5.28)