Die implizite Methode der alternierenden Richtungen

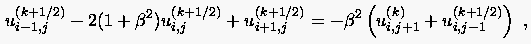
Eine weitere Verbesserungsmöglichkeit liegt in der Methode der alternierenden Richtungen, nach seiner englischen Bezeichnung (alternating direction implicit method) auch hierzulande ADI-Methode genannt. Dieses Verfahren eignet sich sowohl zur Lösung instationärer (vergleiche Kapitel 3.6.1) als auch zur iterativen Lösung elliptischer Gleichungen. Im Falle der iterativen Lösung des elliptischen Problems (5.8) alterniert die Iteration zwischen Seidelschen Linienschritten in $x$-Richtung und daran anschließenden Schritten in $y$-Richtung (sog. sweeps). Beginnt man den Zyklus beispielsweise mit der Lösung aller Linien $y\; =$ konstant, so hat man zunächst das tridiagonale System

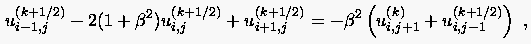(5.29)

und hierauf das analoge System für alle Linien $x\; =$ const.

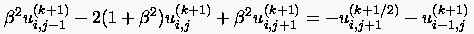(5.30)

zu lösen. Wie wir bereits festgestellt haben, handelt es sich bei den beiden letztgenannten Gleichungen um implizite Formeln, da sie mehr als eine Unbekannte enthalten, jedoch für alle Punkte einer Linie als System, in unserem Beispiel als tridiagonales System, geschlossen zu lösen sind.

Ein Iterationszyklus ist beendet, sobald jede Linie $x\; =$ konst. und jede Linie $y\; =$ konst. erfaßt wurde.

 

Abbildung 44: Illustration der Beziehungen (5.29) und (5.30).

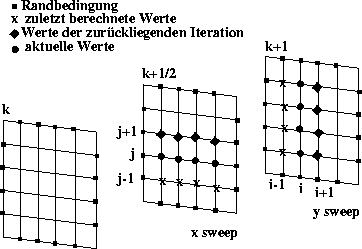Im Vergleich zu dem einfachen Linien-Gauß-Seidel Verfahren kann die Konvergenz mit Hilfe der ADI Methode in vielen Fällen verbessert werden, da die implizite Behandlung und damit ein schneller Informationstransport in beiden Richtungen gewährleistet ist. Ändert sich bei Anwendung eines Linien-Gauß-Seidel Verfahren, das immer in Schleifen von unten nach oben durchlaufen wird, die Randbedingung am oberen Rand, so kann sich die Störung in jedem Iterationsschritt nur um eine Gitterlinie nach unten ausbreiten. Der Informationsfluß und damit die Konvergenz ist deshalb langsam. Beim ADI-Verfahren wäre im gleichen Fall durch den y-sweep immer ein impliziter Halbschritt in vertikaler Richtung vorhanden, und das Verfahren konvergiert damit schneller.

Der Iterationsprozeß läst sich möglicherweise beschleunigen, wenn man gemäß den oben stehenden Ausführungen einen Relaxationsfaktor $$ einführt. Die Systeme (5.29) und (5.30) lauten dann

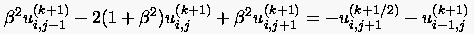(5.31)

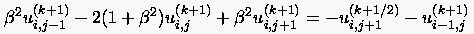(5.32)