Die Jacobische Iterationsmethode

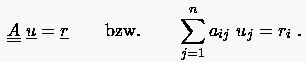
Gelöst werden soll ein beliebieges lineares Gleichungssystem von Typ:

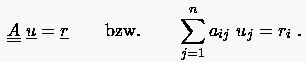(5.13)

Die iterative Berechnung eines neuen Elements ($k+1$) des Unbekanntenvektors geschieht bei der Jacobischen Iterationsmethode durch Auswertung der entsprechenden Zeile des Gleichungssystems unter Verwendung von Nachbarwerten, die stets vom vorherigen Iterationsschritt $k$ genommen werden:

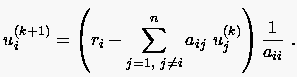(5.14)

Angewendet auf die Lösung der diskretisierten Laplacegleichung (5.8) für alle inneren Punkte lautet die Jacobische Iterationsmethode:

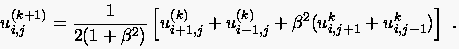(5.15)

Die hier verwendete Vorgehensweise wird auch als Gesamtschrittverfahren bezeichnet, weil das gesamte ''neue'' Feld auf der Basis von ''alten'' Unbekanntenwerten bestimmt wird. Sie wird in der Praxis wenig benutzt, weil die hierbei vektorweise iterierten Werte $$u^(k) langsamer gegen die exakte Lösung $$u konvergieren als bei dem noch zu erläuternden Gauß-Seidel Verfahren. Die Jacobi-Methode ist vor allem von theoretischem Wert. Sie bietet eine gute Vergleichsmöglichkeit zur Beurteilung und Regulierung des Konvergenzverhaltens anderer Methoden.

Bevor wir zu einem weiteren iterativen Verfahren kommen, betrachten wir die FTCS-Diskretisierung der in der Zeit parabolischen PDG (analog zu (3.55) markiert $n$ die Zeitstufe)

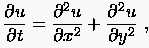(5.16)

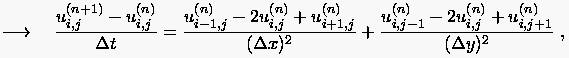(5.17)

für die man mit $$ = 1 un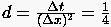d die folgende Darstellung erhält:

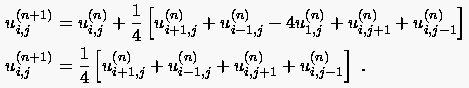(5.18)

Die Analogie zwischen der iterativen Lösung von stationären und instationären elliptischen Problemen wird hier offenkundig. Obwohl die beiden Gleichungen (5.15) und (5.18) zwei völlig verschiedene physikalische Phänomene beschreiben, führen sie für den Sonderfall $$= 1, $d\; =\; 1/4$ auf die selbe Lösungsvorschrift. Den Jacobischen Iterationsprozeß zur Lösung der Laplacegleichung startet man mit einer beliebigen Anfangsverteilung $$u⁽⁰⁾. Die Zwischenlösung der nicht auskonvergierten Verteilungen $$u^(k) (siehe Abblidung 5.28) haben keine physikalische Bedeutung. Bei der Lösung des instationären Problems (5.16) ist die Anfangsverteilung $$u⁽⁰⁾ dagegen durch die dazugehörigen Anfangsbedingungen festgelegt. Im Falle stationärer Randbedingungen streben die Werte $u$_i,j⁽ⁿ⁾ gegen einen stationären Wert, der mit der auskonvergierten Lösung des Jacobischen Iterationsprozesses übereinstimmt.