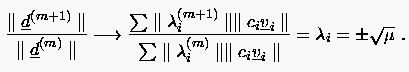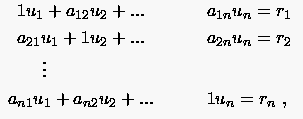
Die numerische Lösung partieller Differentialgleichungen durch finite Approximationen führt auf das mathematische Gebiet der linearen Algebra. In den vorausgegangenen Abschnitten dieses Kapitels haben wir einige Möglichkeiten zur Lösung der anfallenden linearen Gleichungssysteme skizziert. Zur Beurteilung der Verfahren genügen manchmal bereits geringe, grundlegende Kenntnisse der linearen Algebra. Wir werden uns in diesem Abschnitt eingehender mit den Konvergenzeigenschaften der iterativen Lösungsverfahren beschäftigen, ohne den dazugehörigen mathematischen Aufwand allzu groß werden zu lassen.
Man betrachte lineare algebraische Gleichungen
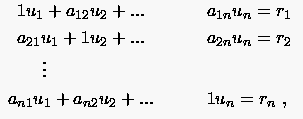
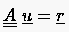 |
(5.36) |
die alle mit den Koeffizienten der Hauptdiagonalen normiert wurden.
Wir wollen annehmen, daß der Wert der Koeffizientendeterminante
von 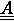 verschieden von Null sei, daß also
verschieden von Null sei, daß also
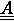 -1 existiert. Nach der Normierung verfügt die
Matrix
-1 existiert. Nach der Normierung verfügt die
Matrix 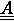 auf der Hauptdiagonalen nur noch über
Elemente vom Wert eins. Daher kann man anstelle von
(5.36) auch
auf der Hauptdiagonalen nur noch über
Elemente vom Wert eins. Daher kann man anstelle von
(5.36) auch
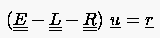 |
(5.37) |
schreiben, wobei
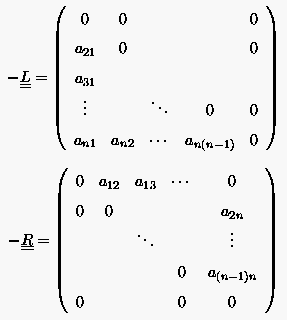
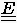 die Einheitsmatrix der Ordnung ist. Eine
Auflösung von (5.37) nach dem unbekannten Vektor
ist durch die Zerlegung besonders einfach
die Einheitsmatrix der Ordnung ist. Eine
Auflösung von (5.37) nach dem unbekannten Vektor
ist durch die Zerlegung besonders einfach
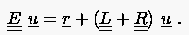
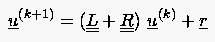 |
(5.38) |
definiert. Für das Punkt-Gauß-Seidel-Verfahren notiert man
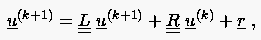 |
(5.39) |
wofür auch
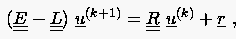
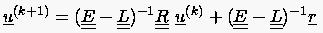 |
(5.40) |
geschrieben werden kann.
Die Matrizen 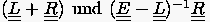 nennt man die der Abbildungsvorschrift
nennt man die der Abbildungsvorschrift
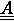 zugeordneten Iterationsmatrizen `
zugeordneten Iterationsmatrizen `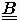 ' von
Jacobi bzw. Gauß-Seidel. Wenn die gesuchte Lösung der Beziehung
(5.38) bzw. (5.39)
' von
Jacobi bzw. Gauß-Seidel. Wenn die gesuchte Lösung der Beziehung
(5.38) bzw. (5.39)
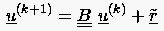 |
(5.41) |
ist (man sagt auch ist Fixpunkt der Gleichung (5.41)), und der Fehler der Näherungslösung des -ten Iterationsschrittes
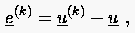
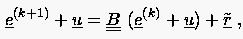
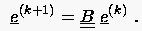
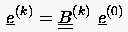 |
(5.42) |
a priori angeben.
Für die sukzessiven Relaxationsverfahren lautet die Iterationsvorschrift
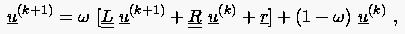
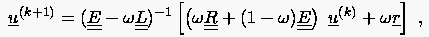 |
(5.43) |
also
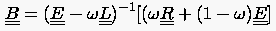 |
(5.44) |
gewinnt.
Analog zum Abschnit 3.2.2 versuchen wir den Fehlervektor
als Linearkombination von Eigenvektoren der
Iterationsmatrix 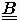 auszudrücken. Vorausgesetzt
auszudrücken. Vorausgesetzt
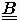 habe linear unabhängige Eigenvektoren
zu den -ten verschiedenen Eigenwerten ,
so kann man die Komponenten des Anfangsfehlers e(0) als Linearkombination der Eigenvektoren in der Form
habe linear unabhängige Eigenvektoren
zu den -ten verschiedenen Eigenwerten ,
so kann man die Komponenten des Anfangsfehlers e(0) als Linearkombination der Eigenvektoren in der Form
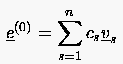
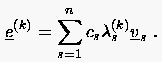 |
(5.45) |
Für die Konvergenz des Iterationsverfahrens ist es notwendig und
hinreichend, daß sämtliche Eigenwerte betragsmäßig
kleiner Eins sind, woraus folgt, daß mit
wachsendem gegen Null strebt. Im Konvergenzfall bestimmt
der betragsmäßig größte Eigenwert, den man als
Spektralradius `rho' von 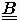 bezeichnet, die
asymptotische Abnahme des Fehlervektors .
bezeichnet, die
asymptotische Abnahme des Fehlervektors .
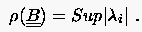
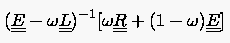
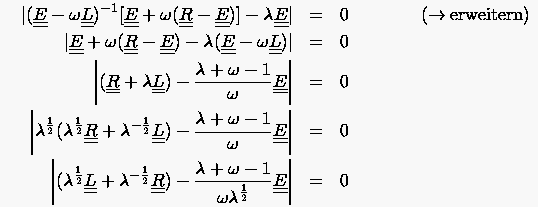
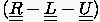 von konsistenter Ordnung
von konsistenter Ordnung
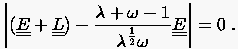 |
(5.46) |
Vergleicht man die Eigenwertaufgabe (5.46) mit derjenigen des Jacobischen Gesamtschrittverfahrens
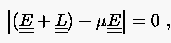
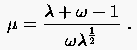 |
(5.47) |
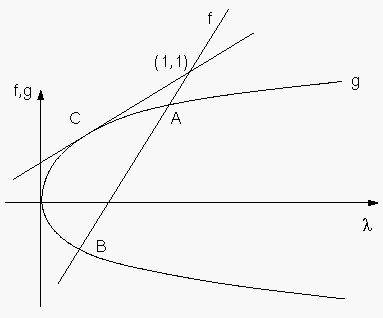
In einer veränderten Fassung läßt sich (5.47) als Schnittpunkt zweier Graphen und darstellen
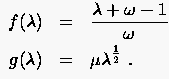
 |
Im Spezialfall des Gauß-Seidelschen Verfahrens mit reduziert sich die Relation (5.47) auf
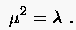
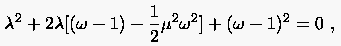
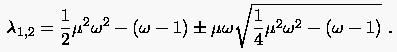 |
(5.48) |
Mit wachsendem Relaxationsfaktor wandern und wegen ihres stetig kleiner werdenden Abszissenunterschiedes aufeinander zu. Die beiden Schnittpunkte vereinigen sich im Berührungspunkt, wenn die Diskriminante
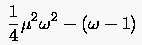
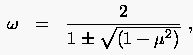 |
(5.49) |
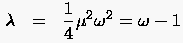 |
(5.50) |
erhalten.
Unser Ziel war es, den größten Eigenwert der Iterationsmatrix (5.43) in Abhängigkeit von zu minimieren. Bereits aus Abbildung 45 wird ersichtlich, daß der Fall zweier verschiedener reeller Wurzeln (5.48) hierfür nicht von Interesse sein kann, da eine der beiden stets größer als ist. Gleiches gilt auch für die konjugiert komplexen Wurzeln
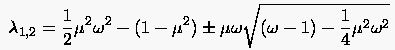 |
(5.51) |
welche in die (5.50) ähnliche Beziehung
münden. Im Unterschied zu (5.50) sind für das Zustandekommen komplexer Wurzeln jedoch größere Relaxationsfaktoren notwendig, so daß wir uns auf die Untersuchung von (5.49) beschränken können.
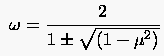 |
(5.52) |
Da der Spektralradius für konvergente Iterationsabläufe stets kleiner als eins sein muß, fordern wir
Deutlich erkennt man, daß die Verwendung des Minuszeichens in (5.49) auf Relaxationsfaktoren führt, wohingegen die von uns gesuchte Lösung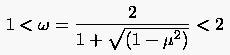
Von entscheidener Bedeutung zur Bestimmung eines optimalen Relaxationsfaktors ist also die Kenntnis des Spektralradius der Jacobischen Iterationsmatrix . Zur Abschätzung des Spektralradius, einer quadratischen Matrix benutzt man häufig den Satz von Gerschgorin. Hiernach kann der Betrag des größten Eigenwertes der quadratischen Matrix die größte Summe der Beträge der Elemente einer Zeile oder Spalte nicht überschreiten.
Beweis: Aus dem Eigenwertproblem
folgt nach Division aller Gleichungen durch die größte Komponente des Eigenvektors für die -te Zeile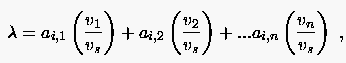
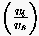 immer < ist, gilt
deshalb
immer < ist, gilt
deshalb
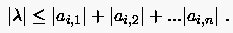 |
(5.53) |
Da die Eigenwerte von 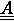 T immer die selben wie die
von
T immer die selben wie die
von 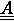 sind, ist der Satz auch für Spalten richtig.
sind, ist der Satz auch für Spalten richtig.
Ein anderer gangbarer Weg zur Bestimmung von ist die Durchführung von Anfangsiterationen mit einem Startwert , woraus sich anschließend eine Näherung des Jacobischen Spektralradius ermitteln läßt. Diese Näherung setzt man in die Beziehung (5.52)
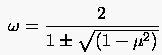
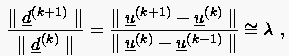 |
(5.54) |
wobei man als Vektornorm für gewöhnlich die euklidische Norm verwendet.
Beweis: Entwickelt man den Anfangsfehler aus den Eigenvektoren der Iterationsmatrix des Gauß-Seidel- Verfahrens,
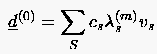
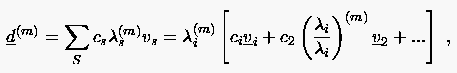
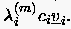 . Deshalb geht
. Deshalb geht