Bemerkungen zum Konditionsproblem

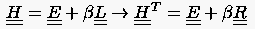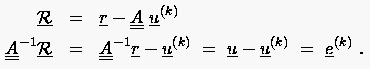
Die Konditionszahl der Systemmatrix $$A ist für die direkten Lösungsverfahren bei gegebener Stellenzahl des verwendeten Rechners maßgebend für die Genauigkeit der berechneten Lösungen, da hierdurch der Verlust an sicheren Stellen bestimmt ist (siehe Einleitung des Kapitels 5). Für die iterativen Verfahren ist die Konditionszahl entscheidend für das Konvergenzverhalten, indem eine große Konditionszahl schlechtes Konvergenzverhalten nach sich zieht.

Wie in Abschnitt 5.2.7 beschrieben, bricht man den Iterationsprozeß zur Bestimmung der Lösung des Systems $$A u = r ab, wenn das Residuum $$R bzw. eine seiner Komponenten eine vorgegebene Schranke unterschreitet:

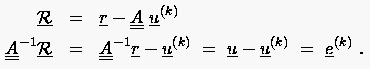(5.55)

Für schlecht konditionierte Matrizen $\{(\{$A A^-1 }>> 1 } kann $$e^(k) noch recht große Komponenten haben. Dies trifft beispielsweise für `nahezu' singuläre Matrizen $$A zu, für die $det($A) gegen Null geht, weswegen die Elemente der inversen von $$A zu großen Werten tendieren.

Grundsätzlich empfiehlt sich eine Überprüfung der Kondition der Systemmatrix $$A, gegebenenfalls sollte man dann den Aufwand zur `Vorkonditionierung' nicht scheuen. Dabei kommt es vor allem auf die geschickte Wahl einer symmetrischen positiv definiten Matrix $$C an, welche sich als Produkt einer regulären Matrix $$H mit ihrer Transponierten darstellt:

Mit Hilfe der Matrix $$H wird das zu lösende Gleichungssystem $$A u = r in die äquivalente Form

bzw.

gebracht. Die Matrix $$H sollte so beschaffen sein, daß die Konditionszahl $$(A*) kleiner als $$(A) ist. Die Ähnlichkeitstransformation von $$A*

zeigt, daß für ein optimales $$C = A die Matrix $$A* ähnlich zur Einheitsmatrix ist und folglich die Konditionszahl Eins wäre.

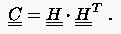
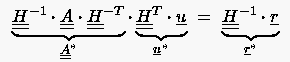
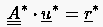
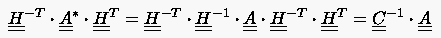
Detaillierte Anleitungen zur Konditionsverbesserung gehen über den augenblicklich möglichen Umfang dieser Unterlagen hinaus. Wir verweisen hierzu auf die entsprechende Fachliteratur aus dem Bereich der numerischen Mathematik. Für symmetrische Matrizen $$A = L + E + R findet man beispielsweise den Vorschlag

mit einem noch geeignet zu wählenden Parameter $$.