Die Methode der konjugierten Gradienten

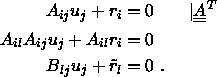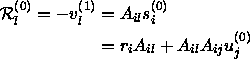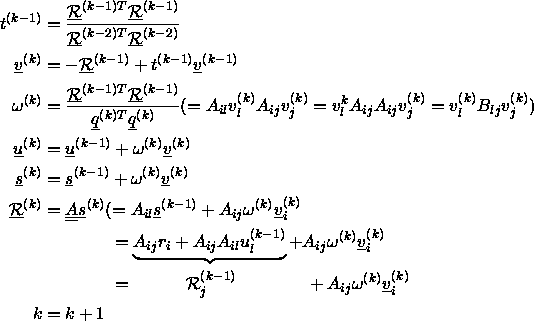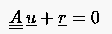
Die Idee dieses Verfahrens ist, daß die Lösung des symmetrisch definierten Systems

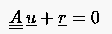(5.56)

zugleich das Funktional

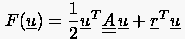(5.57)

wegen

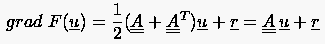(5.58)

minimiert. Man versucht also anstelle der sonst üblichen `gezielten' Lösung von (5.56) das Minimum des quadratischen Funktionals $F$ zu finden. Im Laufe des Verfahrens der konjugierten Gradienten wird dieses Minimum iterativ bestimmt, wobei man zur schrittweisen Verbesserung der aktuellen Lösung $$u^(k) den Gradienten von $F$ verwendet.

Bekanntlich weist der Gradient einer Funktion immer in Richtung der lokal stärksten Zunahme des Funktionswertes. Weil das Funktional zu minimieren ist, zeigt die Auswertung der Beziehung (5.58) für $$u^(k) daher den denkbar ungünstigsten Weg zur Verbesserung der aktuellen Lösung an. Es ist deshalb sehr naheliegend, die dem Gradienten entgegengesetzte Richtung zur Festlegung einer sogenannten Relaxationsrichtung zu verwenden. In dieser unternimmt man dann eine noch zu ermittelnde Anzahl $$ von Einheitsschritten zur Verbesserung der aktuellen Lösung.

Zu Beginn der Iteration bestimmt man aus einer beliebigen Startlösung $$u⁽⁰⁾ eine erste, bessere Näherung $$u⁽¹⁾ gemäß

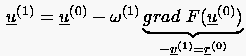(5.59)

$mit$v^(i+k) = Verbesserungsvektor k (k + 1)

R⁽ⁱ⁾ = Residuenvektor von (5.56) .

Die Schrittweite ergibt sich ebenfalls aus der Lösung einer Extremalaufgabe. Sie paßt die Beziehung (5.59) an die Minimumbedingung für $F$ an:

Differenziert man diesen Ausdruck nach $$, so erhält man aus der für extreme $F$ notwendigen Bedingung $$F / = 0 die Relation

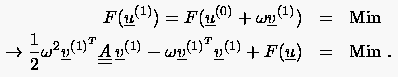
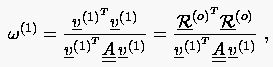(5.60)

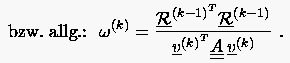(5.61)

Die nun folgenden Iterationsschritte unterscheiden sich ein wenig von dem ersten Schritt. Hierzu betrachte man die folgenden Beziehungen

analog

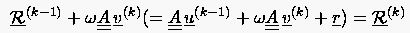
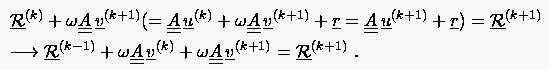(5.62)

Aus der letzten Gleichung läßt sich $$R^(k+1) bereits ohne die Kenntnis von $$v^(k+1) analysieren. Von entscheidender Bedeutung ist dabei der zweite Summand $$A  v^(k), der den Anteil der zuletzt gewählten Relaxationsrichtung an dem ''zukünftigen'' Residuum (= Rest) beziffert. Nun ist es sinnlos, einen Anteil des Residuums nochmals zu erzeugen, indem man $$v^(k+1) ähnlich $$v^(k) wählt. Falls der Anteil der $k$-ten Verbesserung am Gradienten von $F(u(k))$ von Null verschieden ist, sollte man diese Information dahingehend nutzen, die Lösung in der zu diesem Anteil senkrechten Richtung zu verbessern. Wir fordern also

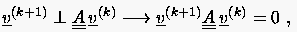(5.63)

worunter die Mathematiker die Konjugiertheit von $$v^(k) und $$v^(k+1) verstehen.

Natürlich verwendet man zur Bestimmung der Verbesserung (Relaxationsrichtung) $$v^(k) auch das zuletzt berechnete Residuum $$R^(k-1), die Konjugiertheit von $$v^(k) und $$v^(k-1) stellt lediglich eine zu erfüllende Nebenbedingung für den Ansatz

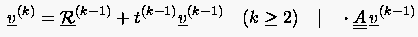(5.64)

mit

also

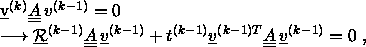
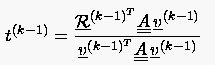(5.65)

dar.

Die Schrittweite $$^(k) ergibt sich wieder aus (5.60). Der Algorithmus vereinfacht sich, wenn man (5.62)

sowie

beachtet. Hieraus erhalten wir

und schließlich für alle $k\; 2$ den allgemeinen Relaxationsschritt

      

Abschließend wollen wir noch die Beschränkung auf symmetrische, definite Koeffizientenmatrizen aufgeben. Zumindest für die Lösung strömungsmechanischer Probleme ist die Erweiterung auf nichtsymmetrische Probleme geboten, weil die finite Approximation von Konvektionstermen stets unsymmetrische Beiträge zur Systemmatrix liefert.

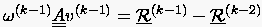
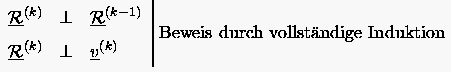
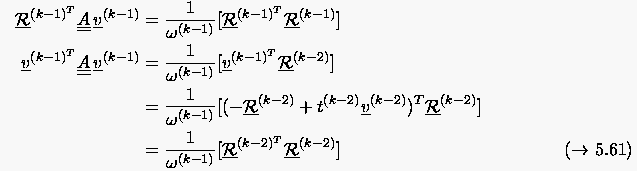
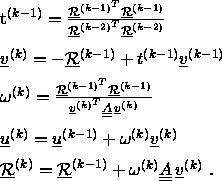
Die einfachste Idee, ein Problem mit unsymmetrischer, nicht positiv definiter Koeffizientenmatrix mit Hilfe des CG-Verfahrens zu lösen, ist, anstelle des ursprünglichen Problems

ein mit $$A^T erweitertes Problem

zu lösen. Das Produkt $$A^T A = B ist für jede nicht singuläre reelle Matrix $$A

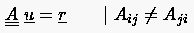
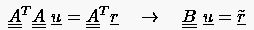
1. quadratisch,
2. positiv definit.

Hieraus ergibt sich eine zweite Anwendungsmöglichkeit dieses Gedankenspiels, nämlich seine Verwendung auf überbestimmte Probleme wie sie z.B. bei der Wirbelstärke-Geschwindigkeitsformulierung der Navier-Stokes Gleichung auftreten:

Die Erweiterung mit $$A^T führt dann auf ein quadratisches Gleichungssystem zur Bestimmung der $m$ unbekannten Komponenten von $$u. Das Ergebnis ist ein Unbekanntenvektor, der das ursprüngliche Problem nicht exakt löst. Die Verteilung des Fehlers auf die einzelnen Komponenten verläuft jedoch so ausgeglichen, daß der quadratische Fehler $$R^TR minimal wird.

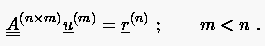
Die faktische Quadrierung der Koeffizientenmatrix ist jedoch extrem rechenintensiv, weswegen man die Koeffizienten von $$B in der Praxis nicht vorab explizit berechnet, sondern die Erweiterung des ursprünglichen Problems direkt in die CG-Prozedur einarbeitet (CG-Ausgleichsverfahren):

Main wählt eine Startlösung $u$_j⁽⁰⁾, bestimmt den Residuenvektor des unsymmetrischen Systems

$s$_i⁽⁰⁾ = r_i + A_ij u_j⁽⁰⁾ ,

sowie eine Verbesserung

und steigt damit in die zweite Position der Prozedur ein.