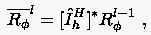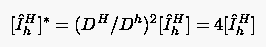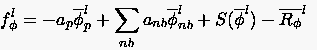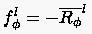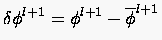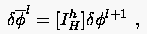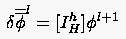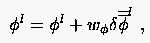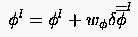Next: Numerische Gittergenerierung
Up: Mehrgitterverfahren
Previous: Restriktions- und Prolongationsoperator
Der prinzipielle Ablauf des Rechenverfahrens wurde bereits in
Abbildung 49 dargestellt. Hier soll das verwendete
Relaxationsverfahren, der Übergang vom Fein- zum
Grobgitter (Pfeil nach rechts unten) und vom Grob- zum Feingitter (Pfeil nach rechts oben)
zusammenfassend beschrieben werden.
Betrachten wir die diskretisierte Form einer Gleichung:
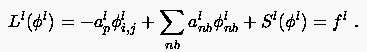 |
(5.95) |
Beim Übergang (Pfeil nach rechts unten) von einer Gitterebene zur Ebene
sind folgende Rechenschritte durchzuführen:
- Die Residuen auf dem Feingitter berechnen:
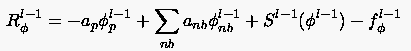 |
(5.96) |
- Restriktion der Lösungen (nur beim FAS)
FAS-Verfahren:
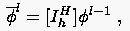 |
(5.97) |
CS-Verfahren:
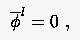 |
(5.98) |
und der Residuen 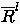 :
:
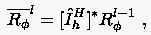 |
(5.99) |
mit
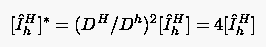
Die Modifikation des Restriktionsoperators kommt daher, daß bei
der finiten Approximation die ursprünglichen Gleichungen mit dem
Quadrat der Schrittweite und der Jacobi-Determinate
multipliziert werden. Während die Jacobi-Determinate auf Grob-
und Feingitter etwa gleichbleibt, vergrößert sich beim
Übergang vom Fein- zum Grobgitter immer um den Faktor 2.
- rechte Seite der Grobgittergleichung :
FAS-Verfahren:
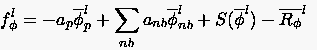 |
(5.100) |
CS-Verfahren:
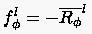 |
(5.101) |
Beim Übergang (Pfeil nach rechts oben) von Gitterbebene zur Ebene sind
durchzuführen:
- Die Berechnung der Grobgitterkorrektur
beim FAS-Verfahren:
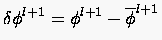 |
(5.102) |
- und ihre Prolongation
FAS-Verfahren:
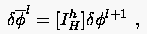 |
(5.103) |
CS-Verfahren:
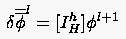 |
(5.104) |
- Korrektur der Lösung auf Feingitter
FAS-Verfahren:
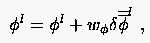 |
(5.105) |
CS-Verfahren:
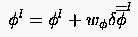 |
(5.106) |
Es handelt sich hierbei um iterative
Verfahren, deren Grundgedanke in Hinblick auf ihre konkrete
Anwendung weniger Einschränkungen erfährt. Charakteristisch für
MGM ist die gleichzeitige Diskretisierung der zu lösenden DGL auf
verschiedenen Gittern unterschiedlicher Maschenweite
(typischerweise ).
Dies gestattet die Ausnutzung der jedem Gitter eigenen Information
über die Lösung des Problems. Hierin liegt der Hauptgrund für
die hohe Effektivität von MGM.
Neben Flexibilität und Schnelligkeit weisen MGM weitere
vorteilhafte Merkmale auf:
- 1
- Sehr natürlich ist bei MGM eine Selbststeuerung
bei der Gittererzeugung. Insbesondere sind lokal
begrenzte Gitterverfeinerungen möglich, etwa
im Bereich von Singularitäten der Lösung.
- 2
- Bei geeigneter Implementierung läßt sich MGM auch
direkt zur Lösung nichtlinearer Aufgaben einsetzen
(sog. full approximation scheme ''FAS'').
- 3
- Die für MGM typische, gleichzeitige Benutzung
mehrerer Gitter gestattet ohne wesentlichen
Mehraufwand die Durchführung von Extrapolationen.
- 4
- Es treten praktisch keine numerischen
Stabilitätsschwierigkeiten auf, wie sie bei manchen
direkten Lösern zu beobachten sind.




Next: Numerische Gittergenerierung
Up: Mehrgitterverfahren
Previous: Restriktions- und Prolongationsoperator
Benjamin Gilde
Sat Dec 16 15:24:45 CET 2000
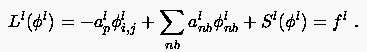
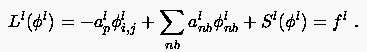
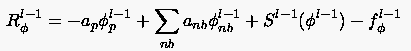
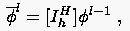
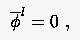
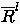 :
: