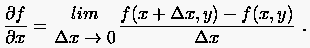
Der Einsatz digitaler Rechenautomaten beschränkt sich auf algebraische Probleme. Um eine PDG mit numerischen Methoden zu lösen, müssen daher alle auftretenden partiellen Ableitungen durch algebraische Ausdrücke ersetzt werden. Solche Ausdrücke heißen endliche bzw. finite Differenzenformeln. Die Idee der finiten Differenzenformeln geht auf die Einführung der Ableitung für stetige Funktionen zurück:
 |
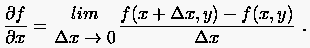(2.1) |
Erfahrungsgemäß stellt schon der Differenzenquotient
 |
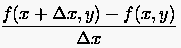(2.2) |
eine befriedigende Näherung für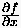 
dar, sofern die Schrittweite ``hinreichend'', jedoch
nicht unendlich
klein gewählt wird. Ersetzt man sämtliche partielle Ableitungen der
PDG durch geeignete Formeln der Gestalt (2.2), so reduziert sich
das ursprünglich kontinuierlich gestellte Problem auf wenige
Kontrollpunkte. Man spricht daher von Diskretisierung der DGL auf
der Basis finiter Differenzen.
Die Stützstellen der Differenzenformeln werden nicht explizit, sondern durch die Knotenpunkte eines automatisch erzeugten Gitters bestimmt (Abb. 15).
 |
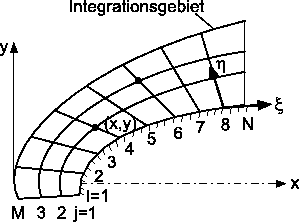Die Generierung solcher Gitter wird in einem eigenen Kapitel behandelt, trotzdem wollen wir hier einiges zur Beschaffenheit des Gitters und zur Wahl geeigneter Koordinaten erwähnen. Zufriedenstellende Lösungen erhält man nur, wenn das zugrunde gelegte Gitter sowohl innerhalb des Integrationsgebietes als auch entlang seiner Berandung physikalische Bindung behält. Wichtige Kriterien sind das Auflösungsvermögen des Gitters bezüglich der im Integrationsgebiet auftretenden Gradienten und der Integrationsbedingungen.
In Kapitel 1 wurde gezeigt, wie sich die Lösung der PDG entlang natürlicher Koordinaten vereinfachen kann. Die natürlichen Koordinaten verlaufen im kartesischen Bezugssystem meist krummlinig. In diesem System ist die Formulierung der finiten Differenzengleichung (FDG) für ein an natürlichen Koordinaten orientiertes Gitter unzweckmäßig. Die Ausdrücke werden unnötig kompliziert und führen wegen der unregelmäßigen Schrittweite zu Schwierigkeiten bei der Lösung der PDG. Die Probleme können überwunden werden, wenn man anstelle des kartesischen Bezugssystems eine natürliche Basis verwendet. Der Zusammenhang zwischen beiden Basissystemen ist durch Transformationsformeln wiedergegeben
 |
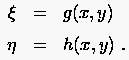
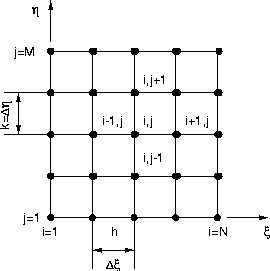Die Lage der Gitterpunkte wollen wir fortan mit in -Richtung bzw.\ in -Richtung bezeichnen. Die Anzahl der betrachteten Punkte in - bzw. -Richtung seien und . Die finite Differenzenformulierung der partiellen DGL wird für jeden Gitterpunkt notiert, das entstehende Gleichungssystem hängt vom Typ der DGL ab (siehe Kapitel 1). Während Gleichgewichtsprobleme auf ein System simultan zu lösender finiter Differenzengleichungen führen, können die FDG eines Ausbreitungsproblems hintereinander gelöst werden. Das Ergebnis beider Fälle sind die Werte der abhängigen Variablen an allen Gitterpunkten.