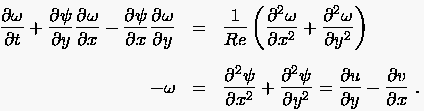Next: Finite Differenzenmethoden
Up: Klassifizierung partieller Differentialgleichungen (PDG)
Previous: Anfangs- und Randbedingungen
Die Formulierung einer PDG öheißt konservativ, wenn die Ableitungen einer
Variablen nicht explizit aufgeführt sind. Die Gleichungen
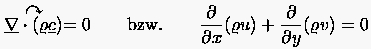
sind konservativen Formulierungen des Massenerhaltungssatzes für stationäre
Strömungen. Die nichtkonservative Form lautet
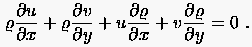
Notiert man eine Bilanzgleichung mit Hilfe der ``ursprünglichen'' Variablen
(, , , ), so spricht man auch von einer Formulierung auf der
Basis primitiver Variablen. Für die 2-dimensionale N-S-Gleichung lautet
diese:
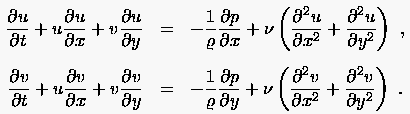
In der Regel bevorzugt man jedoch Formulierungen auf der Basis abgeleiteter
Größen 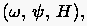 , wie z.B. die Wirbelstärke - Stromformulierung
der 2-dimensionalen N-S-Gleichung
, wie z.B. die Wirbelstärke - Stromformulierung
der 2-dimensionalen N-S-Gleichung
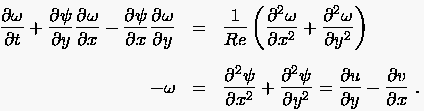




Next: Finite Differenzenmethoden
Up: Klassifizierung partieller Differentialgleichungen (PDG)
Previous: Anfangs- und Randbedingungen
Benjamin Gilde
Sat Dec 16 15:24:45 CET 2000
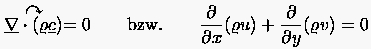
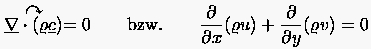
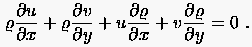
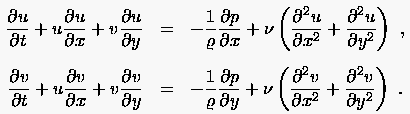
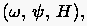 , wie z.B. die Wirbelstärke - Stromformulierung
der 2-dimensionalen N-S-Gleichung
, wie z.B. die Wirbelstärke - Stromformulierung
der 2-dimensionalen N-S-Gleichung