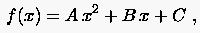
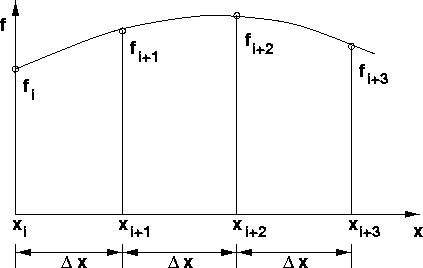
Polynomgestützte Methoden

Polynomgestützte Methoden bieten eine zweite Möglichkeit zur Entwicklung finiter Differenzenformeln. Sie basieren auf der Annahme, daß der Verlauf der abhängigen Variablen in dem betrachteten Bereich durch ein Polynom wiedergegeben wird. Hierzu betrachten wir das Polynom 2. Ordnung

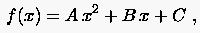(2.18)

dessen zunächst unbekannte Koeffizienten durch die Funktionswerte an drei äquidistanten Stützstellen $x$_i = 0, $x$_i+i = x und $x$_i+2 = 2 x

bestimmt werden. Die Auflösung des Gleichungssystems liefert die Werte

Hiermit lassen sich die partiellen Ableitungen

auswerten.

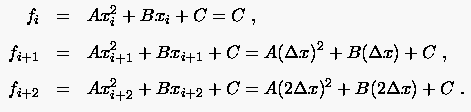
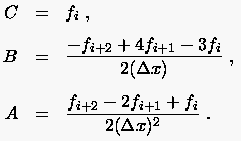
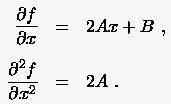
Beispielsweise erhält man für 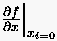die finite Differenzenformulierung

also den vorwärtigen Differenzenquotienten von der Ordnung $($x)². Die Näherung der zweiten Ableitung

entspricht ebenfalls einem schon bekannten vorwärtigen Differenzenquotienten (2.10).

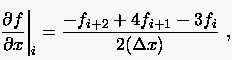
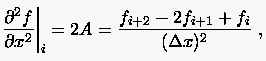
Am Beispiel der vorwärtigen Differenzenformulierung 1. Ordnung für 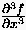lassen sich die unterschiedlichen Entwicklungsmethoden vergleichen.

 

Abbildung 19: Veranschaulichung der Gleichung (2.19).

a)

Die Taylorreihenentwicklungen zu den Schrittweiten $$x, $2$x, $3$x lauten:

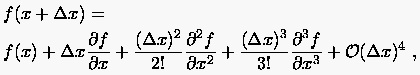(2.19)

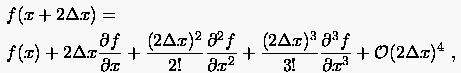(2.20)

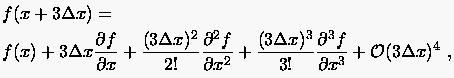(2.21)

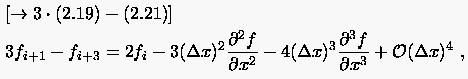(2.22)

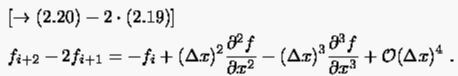(2.23)

Aus $[(2.22)+3(2.23)]$ erhält man aufgelöst nach der dritten partiellen Ableitung

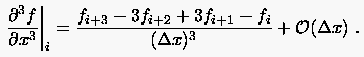(2.24)

b)

Schreibt man die Rekursionsformel

aus, so ergibt sich

und somit

c)

Betrachtet wird das Polynom dritter Ordnung

Für 4 äquidistante Stützstellen $x$_i = 0, $x$_i+n=x_i + nx; $n\; =\; 1...3$ berechnen sich die Koeffizienten gemäß

zu

Die partiellen Ableitungen des Polynoms sind bestimmt durch

womit die gesuchte finite Differenzenformulierung wiederum

lautet. Zusätzlich wollen wir hier noch bemerken, daß die Näherung der ersten partiellen Ableitung in $x$_i mit dem Koeffizienten $C$ zusammenfällt

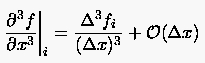
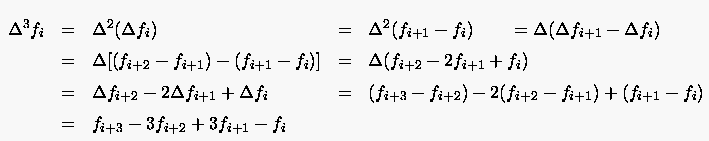
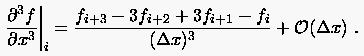
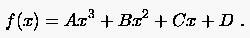
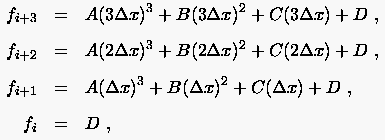
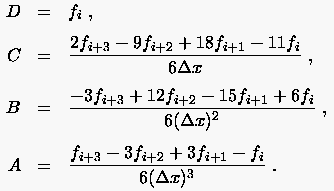
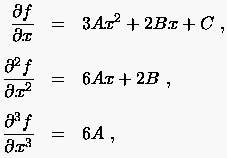
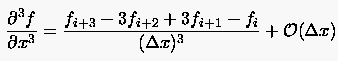
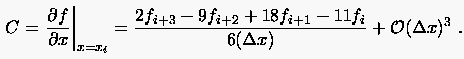(2.25)

Für die am Ende des Kapitels tabellarisch wiedergegebenen finite Differenzenformulierungen höherer partieller Ableitungen sei hier exemplarisch eine rückwärtige Formulierung der ersten partiellen Ableitung hergeleitet. Hierzu formulieren wir zunächst eine erste rückwärtige Entwicklung der analytischen Funktion $f(x)$ zur Schrittweite $$x

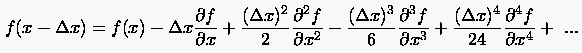(2.26)

Im gewählten Beispiel soll die gesuchte Differenzenformel die erste partielle Ableitung einschließlich der in der Schrittweite von 2. Ordnung kleinen Gliedern genau annähern. Die obige Entwicklung (2.13) wird daher nach dem vierten Summanden abgebrochen und man notiert für die Auflösung nach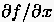

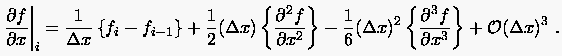(2.27)

Um die geforderte Genauigkeit zu erreichen, müssen die beiden verbleibenden partiellen Ableitungen 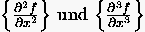durch finite Differenzen von der Ordnung 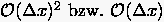ersetzt werden. Diese Differenzenformeln erhält man aus zwei weiteren rückwärtigen Entwicklungen

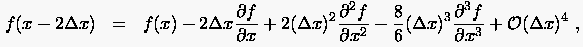(2.28)

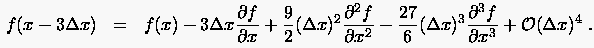(2.29)

Eliminiert man die Glieder der gesuchten ersten Ableitung durch geeignete Linearkombinationen (3$$ (2.26) - (2.29) bzw. 2$$ (2.26) - (2.28)), so ergeben sich zwei Bestimmungsgleichungen für die zu ersetzenden partiellen Ableitungen

Diese führen auf die Differenzenformeln

womit man anstelle (2.27)

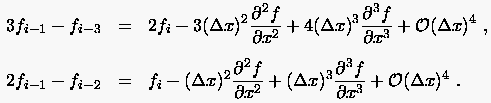
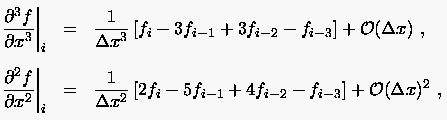
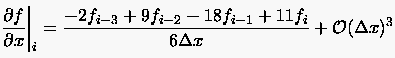(2.30)

notiert.