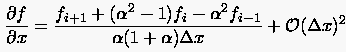Next: Gemischte partielle Ableitungen
Up: Herleitung finiter Differenzenformeln
Previous: Polynomgestützte Methoden
Abschließend erweitern wir die o.a. Methoden auf Rechengitter deren
Schrittweitenfolgen dem Bildungsgesetz
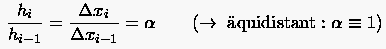
genügen. Wir werden uns der besseren Übersicht halber auf das Beispiel
des zentralen Differenzenquotienten 2. Ordnung für 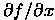 beschränken.
beschränken.
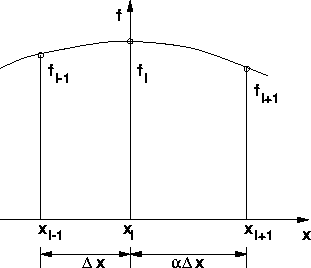
Abbildung 20: Nichtäquidistantes Gitter.
 |
Die Entwicklungen der Funktion um lauten
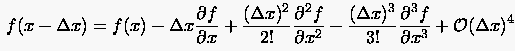 |
(2.31) |
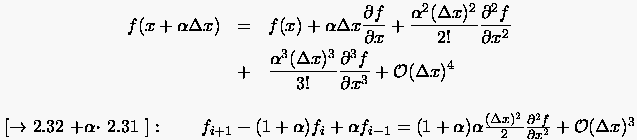 |
(2.32) |
bzw.
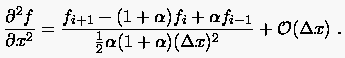
Setzt man diese Näherung der zweiten Ableitung in (2.31) ein und
löst nach 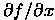 auf, so ergibt sich schließlich an der Stelle
auf, so ergibt sich schließlich an der Stelle
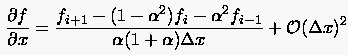 |
(2.33) |
ein Ergebnis, das man auch aus der Betrachtung des quadratischen
Polynoms (Abb. 20)
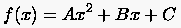
an den Stützstellen 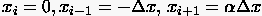 erhält. Aus
erhält. Aus
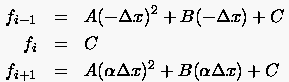
bestimmt man die Koeffizienten zu
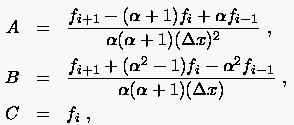
womit sich für 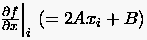 wiederum die Näherung
wiederum die Näherung
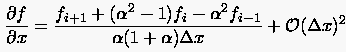 |
(2.34) |
ergibt.




Next: Gemischte partielle Ableitungen
Up: Herleitung finiter Differenzenformeln
Previous: Polynomgestützte Methoden
Benjamin Gilde
Sat Dec 16 15:24:45 CET 2000
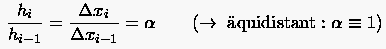
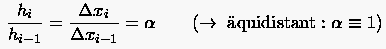
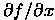 beschränken.
beschränken.

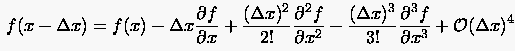
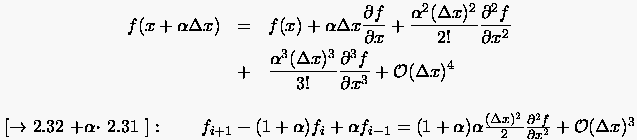
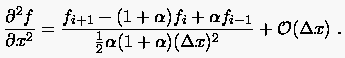
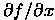 auf, so ergibt sich schließlich an der Stelle
auf, so ergibt sich schließlich an der Stelle
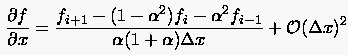
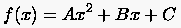
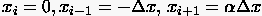 erhält. Aus
erhält. Aus
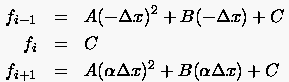
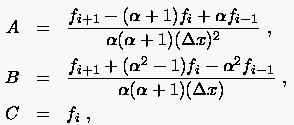
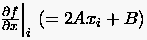 wiederum die Näherung
wiederum die Näherung