Transfinite Interpolation

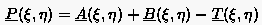
Hier werden die beiden Scherungstransformationen und die Tensor-Produkt-Transformation derart kombiniert, daß durch die resultierende Beziehung ein strukturiertes Netz auf der betrachteten Fläche unter der Bedingung erzeugt wird, daß die Randkurven exakt erfaßt werden (Abb. 72).

Die Vektorsumme $A\; +\; B$ der Gleichung ( 6.101) enthält sowohl alle vier vorgegebenen Randkurven als auch die Verbindungsgeraden zwischen den jeweils benachbarten Eckpunkten der Flächen, wie eine Auswertung von $A\; +\; B$ für die Randparameterwerte $$= 0,1 und $$= 0, 1 zeigt. Dies macht auch eine Betrachtung von Abbildung 73 deutlich. Andererseits erzeugt die Tensor-Produkt-Transformation $T$ der Gleichung (6.102), wie gesehen, ebenfalls geradlinige Koordinatenverläufe, also auch an den vier Rändern. Es liegt deshalb nahe, $T$ von $A\; +\; B$ zu subtrahieren und auf diese Weise eine neue Transformation $P$ zu konstruieren.

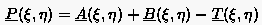(6.103)

In der Tat liegt der durch $P$ erzeugte Punkt für alle Parameterwerte $$ und $$ auf der Fläche, die durch die Randkurven aufgespannt wird. Da Gleichung (6.103) eine Interpolation zwischen der geschlossenen Randkurve darstellt, wobei die Randkurve als kontinuierliche Funktion eine unendliche Anzahl von Punkten enthält, wird die Transformation $P$ auch als Transfinite Interpolation bezeichnet. Damit wird die Möglichkeit der Einbeziehung unendlich vieler Punkte in die Interpolation zum Ausdruck gebracht, im Gegensatz zu lediglich vier Eckpunkten bei der bilinearen Tensor-Produkt-Transformation.

Abschließend sei noch bemerkt, daß der Transfiniten Interpolation statt der Scherungstransformation aus der Lagrange-Interpolation (6.101) auch die Hermitesche Interpolation zugrunde gelegt werden kann. Die Benutzung der Hermiteschen Interpolation ist insbesondere dann von Interesse, wenn Randorthogonalität eine wichtige Rolle spielt. Wie schon dargestellt, ist die Ableitung des Kurvenpunktes nach dem Parameter ein Vektor tangential zur Kurve. Randorthogonalität bedeutet nun, daß dieser Vektor dem Normalenvektor $n$ auf der Berandungskurve entspricht. Wird der Tangentialvektor $t$ an die Randkurve aus deren gegebener Punkteverteilung berechnet, dann folgt der Normalenvektor $n$ aus der Beziehung $n\; t\; =\; 0$.