Modifikation der Scherungstransformation

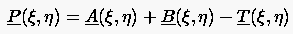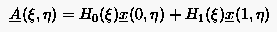
Die einfache Scherungstransformation (6.101) bzw. die darauf basierende Transfinite Interpolation (6.103) kann zu sehr ungünstigen Gitterpunkteverteilungen oder sogar zu Überschneidungen von Gitterlinien führen. In solchen Fällen kann eine Modifikation der Scherungstransformation Abhilfe schaffen. Dabei werden die linearen Interpolationsfunktionen $L$₀ und $L$₁ in der Scherungstransformation durch andere Funktionen $F$₀ und $F$₁ ersetzt. Dabei soll beachtet werden, daß die Summe von $F$₀ und $F$₁ eins ergibt und die Funktion selbst monoton zwischen 0 und 1 verläuft.

Eine Möglichkeit ist es, ohne Einschränkung der Allgemeingültigkeit $L($) durch $H($) in der Gleichung (6.101)

zu ersetzen. Das führt zur dichteren Verteilung der Gitterpunkte im randnahen Bereich.

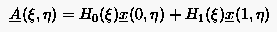
Eine weitere Vorgehensweise ist in den folgenden Gleichungen gegeben (als Beispiel die Scherungstransformation in der $$-Richtung):

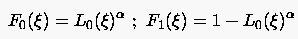(6.104)

oder

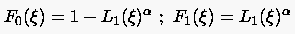(6.105)

Dabei sollte $F$₁() etwa die Verteilungsfunktion an den Randkurven $x\; ($, 0 ) und $x\; ($, 1 ) wiedergeben.

Abbildung 75: Modifizierte Scherungstransformation und die Verteilung der Randgitterpunkte

Von dieser Idee ausgehend, können wir folgende Scherungstransformation konstruieren:

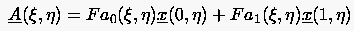(6.106)

mit

Es kann leicht festgestellt werden, daß $A\; ($,0) der Randpunkteverteilung des Südrands und $A\; ($,1) der des Nordrands entspricht.

Analog für die Scherungstransformation in der $$-Richtung:

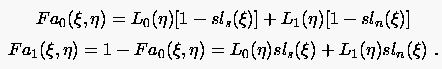
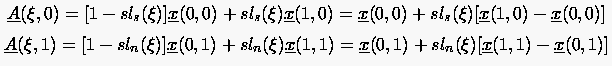
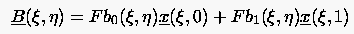(6.107)

mit

Anstelle der Tensor-Produkt-Transformation $(\; B\; A\; )\; ($, ) kann folgende Transformation verwendet werden:

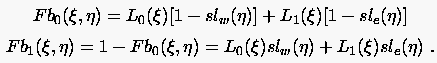
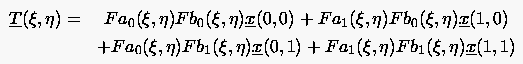(6.108)

Die Transfinite Interpolation setzt sich dann zusammen aus: