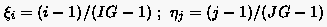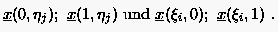
Die Methoden der algebraischen Gittergenerierung vermitteln einen direkten funktionalen Zusammenhang zwischen den Punkten des physikalischen Gebiets, gekennzeichnet durch die kartesischen Koordinaten , und den jeweils zugeordneten Punkten im Rechengebiet, die durch die Koordinaten gegeben sind. Bei der Klasse von algebraischen Methoden, die weitestgehende Kontrolle über das Gitter erlauben, handelt es sich um Methoden, die auf Interpolationspolynomen basieren, die im letzten Kapitel ausführlich behandelt wurden.
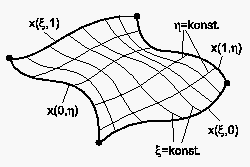
Wir betrachten zunächst eine gekrümmte Fläche im physikalischen Raum, die von vier Randkurven begrenzt wird. Auf den Randkurven sei jeweils die gleiche Anzahl von Randgitterpunkten in beiden Richtungen verteilt. Während eine Kurve durch einen einzigen Parameter beschrieben wird, benötigt die vollständige Beschreibung einer Fläche die Darstellung in zwei unabhängigen Parametern und . D.h., die Fläche wird von zwei unabhängigen Scharen von Koordinatenlinien aufgespannt, entlang denen jeweils der Wert eines Parameters variiert, während der andere Parameter konstant ist. Den Verlauf dieser Koordinatenlinien zu finden, ist Gegenstand der zweidimensionalen Interpolation.
 |
Die Koordinaten und werden hier mit den Laufindizes der Randgitterpunkte und definiert: