Scherungstransformation

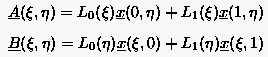
Unter Scherungstransformation verstehen wir die Lagrangesche Interpolation durch zwei Stützstellen. Zwischen jeweils zwei Randpunkten werden zwei Scherungstransformationen in der $$- und $$-Parameter- bzw. Koordinatenrichtung definiert.

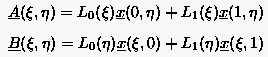(6.101)

$$ und $$ spannen im Parameterraum die Einheitsfläche auf, d.h. $$ Element von [0,1] und $$ Element von [0,1] .

Der Verlauf der Koordinatenlinien ist in Abbildung 73 dargestellt.

Abbildung 73: Verlauf der Koordinatenlinien aus der Scherungs-Transformation

  
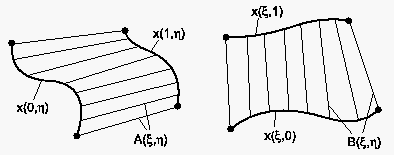Abbildung 73: Verlauf der Koordinatenlinien aus der Scherungs-Transformation

Man erkennt, daß keine der Transformationen aus der Gleichung (6.101) in der Lage ist, alle vier Randkurven zu reproduzieren. Vielmehr erzeugen beide einen geraden Koordinatenlinienverlauf jeweils an den Rändern, deren Randkurven sie nicht erfassen können. Die Ursache hierfür liegt in der Tatsache, daß die Transformationen $A\; ($,) und $B\; ($,) gemäß ihrer Konstruktion unabhängig voneinander sind und nur in den vier Eckpunkten der Fläche für gleiche Parameterwerte das gleiche Ergebnis liefern.