Tensor-Produkt-Transformation

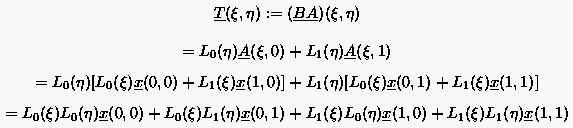
Eine Transformation, die in gewissem Sinne die beiden Gleichungen in (6.101) miteinander kombiniert, ist die Tensor-Produkt-Transformation $T\; ($,) . Sie ist die sukzessive Anwendung der Scherungstransformation $B\; ($,) auf das Ergebnis der Transformation $A\; ($,) ; d.h., $x\; ($,0) und $x\; ($, 1) werden ersetzt durch $A\; ($,0) und $A\; ($, 1) .

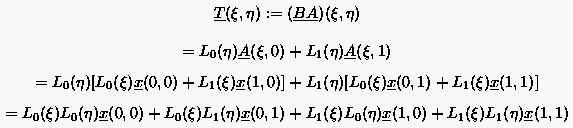(6.102)

Man kann sich leicht davon überzeugen, daß die umgekehrte Transformation $T\; ($,) := ( A B ) (,) zum gleichen Ergebnis führt. Gleichung (6.102) stellt eine bilineare Transformation zwischen den vier Eckpunkten $x\; (0,0)$, $x\; (1,0)$, $x\; (0,1)$ und $x\; (1,1)$ dar. Wie Abbildung 74 zeigt, verlaufen die beiden Koordinatenlinienscharen $$=const. und $$=const. geradlinig.

  
Abbildung 74: Bilineare Tensor-Produkt-Transformation zwischen den Eckpunkten