

Nächste Seite: Instationäre Strömungsstrukturen im Nachlauf
Aufwärts: Instationäre Strömungsstrukturen im Nachlauf
Vorherige Seite: Gitter
Alle Simulationen von Gurney-Flaps werden instationär durchgeführt,
da das Hauptinteresse den Strukturen im Nachlauf gilt. Betrachtet wird
eine Reynoldszahl von 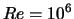 .
Die durchgeführte Zeitschrittkonvergenzstudie zeigt, dass
mit
.
Die durchgeführte Zeitschrittkonvergenzstudie zeigt, dass
mit
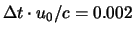 eine sehr feine zeitliche Diskretisierung
gewählt werden muss, um die auftretenden kleinen Zeitmaße auflösen zu
können. Die im Vergleich zu den globalen Strömungsabmessungen
ebenfalls sehr kleinen Strukturen erfordern extrem lange Rechenzeiten, bis
das gesamte Strömungsfeld einen im Mittel konstanten Zustand erreicht hat.
eine sehr feine zeitliche Diskretisierung
gewählt werden muss, um die auftretenden kleinen Zeitmaße auflösen zu
können. Die im Vergleich zu den globalen Strömungsabmessungen
ebenfalls sehr kleinen Strukturen erfordern extrem lange Rechenzeiten, bis
das gesamte Strömungsfeld einen im Mittel konstanten Zustand erreicht hat.
Abbildung:
Aufgelöste Polare für unterschiedliche Gurney-Flaps
links: am HQ17; rechts: am NACA4412.
|
|
Die aufgelösten Polaren werden für beide Profile und unterschiedliche
Gurney-Flaps in Abbildung ![[*]](crossref.png) dargestellt. Es zeigt sich
deutlich, dass der Auftriebsbeiwert bei beiden Profilen mit der Länge des
Gurney-Flaps ansteigt. Der Gewinn an Auftrieb bleibt dabei über einen breiten
Anstellwinkelbereich (
dargestellt. Es zeigt sich
deutlich, dass der Auftriebsbeiwert bei beiden Profilen mit der Länge des
Gurney-Flaps ansteigt. Der Gewinn an Auftrieb bleibt dabei über einen breiten
Anstellwinkelbereich (
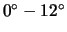 bei NACA4412)
(
bei NACA4412)
(
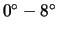 bei HQ17) konstant. Neben dem deutlich wachsenden
Auftrieb ist zu beobachten, dass der Zuwachs mit steigender Höhe des
Gurney-Flaps
abnimmt. Dieses Verhalten wird von den experimentellen Untersuchungen
bestätigt, wobei die gute Übereinstimmung auch die
Qualität des verwendeten LLR
bei HQ17) konstant. Neben dem deutlich wachsenden
Auftrieb ist zu beobachten, dass der Zuwachs mit steigender Höhe des
Gurney-Flaps
abnimmt. Dieses Verhalten wird von den experimentellen Untersuchungen
bestätigt, wobei die gute Übereinstimmung auch die
Qualität des verwendeten LLR 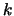 -
-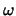 Modells unterstreicht.
Die integrale Wirkung von Gurney-Flaps steht im Zusammenhang mit dem
Abströmwinkel hinter dem Profil. Zwar gilt
die Kutta'sche Abflussbedingung, doch ist deren Anwendung auf
Profile mit stumpfen Hinterkanten oder solchen mit Gurney-Flaps nicht
eindeutig, da sich die Abströmrichtung nicht zwangsläufig aus der Geometrie
ergibt. Die Vergrößerung des Abströmwinkels
Modells unterstreicht.
Die integrale Wirkung von Gurney-Flaps steht im Zusammenhang mit dem
Abströmwinkel hinter dem Profil. Zwar gilt
die Kutta'sche Abflussbedingung, doch ist deren Anwendung auf
Profile mit stumpfen Hinterkanten oder solchen mit Gurney-Flaps nicht
eindeutig, da sich die Abströmrichtung nicht zwangsläufig aus der Geometrie
ergibt. Die Vergrößerung des Abströmwinkels 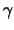 kann jedoch im
nahen Nachlauf ausgewertet werden (Abb.
kann jedoch im
nahen Nachlauf ausgewertet werden (Abb. ![[*]](crossref.png) ).
Diese Veränderung des Abströmwinkels und damit der Zirkulation bewirkt
potentialtheoretisch eine Veränderung des Auftriebs, wobei
ein linearer Zusammenhang zwischen Abströmwinkel und Auftrieb besteht,
während der Widerstand etwa quadratisch vom Abströmwinkel abhängt.
).
Diese Veränderung des Abströmwinkels und damit der Zirkulation bewirkt
potentialtheoretisch eine Veränderung des Auftriebs, wobei
ein linearer Zusammenhang zwischen Abströmwinkel und Auftrieb besteht,
während der Widerstand etwa quadratisch vom Abströmwinkel abhängt.
Abbildung:
Stromlinien im mittleren Strömungsfeld
und Abströmwinkel 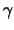 hinter dem HQ17-Profil,
links: mit Gurney-Flap
hinter dem HQ17-Profil,
links: mit Gurney-Flap 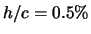 (oben) und
mit Gurney-Flap
(oben) und
mit Gurney-Flap 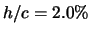 (unten).
rechts: Auftriebs- und Widerstandsbeiwert in
Abhängigkeit vom Abströmwinkel
(unten).
rechts: Auftriebs- und Widerstandsbeiwert in
Abhängigkeit vom Abströmwinkel 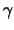 .
.
|
|
Es zeigt sich, dass der Auftriebsbeiwert bereits von einer stationären
Simulation vergleichsweise genau wiedergegeben wird, eine Vorhersage des
Widerstands dagegen in jedem Fall eine instationäre Betrachtung erfordert.
Hier spielen die instationären Strömungsstrukturen im Nachlauf eine große
Rolle, die sich nur im zeitabhängigen Fall erfassen lassen.
Wie vermutet steigen mit anwachsender Länge des Gurney-Flaps sowohl
Auftrieb als auch Widerstand. Dieser Sachverhalt ist in den Polaren
deutlich zu erkennen (Abb. ![[*]](crossref.png) ). Dabei
fällt besonders auf, dass der relative Widerstandszuwachs bei beiden Profilen
im unteren Anstellungsbereich (
). Dabei
fällt besonders auf, dass der relative Widerstandszuwachs bei beiden Profilen
im unteren Anstellungsbereich (
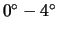 ) mit längeren
Gurney-Flaps
wesentlich größer ausfällt, als mit den kurzen. Dies verändert sich
offensichtlich im oberen Anstellwinkelbereich. Allerdings dominiert bei
hoher Anstellung der Einfluss der Ablösung im Hinterkantenbereich auf der
Oberseite.
) mit längeren
Gurney-Flaps
wesentlich größer ausfällt, als mit den kurzen. Dies verändert sich
offensichtlich im oberen Anstellwinkelbereich. Allerdings dominiert bei
hoher Anstellung der Einfluss der Ablösung im Hinterkantenbereich auf der
Oberseite.
Abbildung:
Widerstandspolare für unterschiedliche Gurney-Flaps,
links: am HQ17; rechts: am NACA4412.
|
|
Das HQ17-Profils hat eine stumpfe
Hinterkante mit 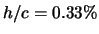 , während das NACA4412-Profil spitz ausläuft.
Trotzdem ist die Abhängigkeit der Beiwerte von der Höhe des Gurney-Flaps
qualitativ vergleichbar.
Der Einfluss des Gurney-Flaps auf den Auftrieb ist beim NACA4412 allerdings
wesentlich stärker als beim HQ17. Insgesamt
ist die Auswirkung des verhältnismäßig kleinen Gurney-Flaps auf den
Auftrieb beachtlich. So steigert ein Gurney-Flap am NACA4412-Profil den
Auftrieb bis zu 110% und am HQ17-Profil bis zu 57%.
Der Einfluss auf den Widerstand ist hingegen beim HQ17 bedeutend
stärker als beim NACA4412. Er wächst um 80% beim NACA4412 und um 110%
beim HQ17.
Im Widerstand ist keine gute Übereinstimmung mit den Experimenten zu
beobachten. Zwar wird der Verlauf qualitativ in gleicher Weise erfasst, das
Niveau unterscheidet sich jedoch deutlich. Die Ursache dafür liegt zum
einen im Experiment, wo aufgrund von 3D-Effekten und des Messverfahrens mit
Fehlern zu rechnen ist, und zum anderen im numerischen Verfahren, da die
Vorhersage von
, während das NACA4412-Profil spitz ausläuft.
Trotzdem ist die Abhängigkeit der Beiwerte von der Höhe des Gurney-Flaps
qualitativ vergleichbar.
Der Einfluss des Gurney-Flaps auf den Auftrieb ist beim NACA4412 allerdings
wesentlich stärker als beim HQ17. Insgesamt
ist die Auswirkung des verhältnismäßig kleinen Gurney-Flaps auf den
Auftrieb beachtlich. So steigert ein Gurney-Flap am NACA4412-Profil den
Auftrieb bis zu 110% und am HQ17-Profil bis zu 57%.
Der Einfluss auf den Widerstand ist hingegen beim HQ17 bedeutend
stärker als beim NACA4412. Er wächst um 80% beim NACA4412 und um 110%
beim HQ17.
Im Widerstand ist keine gute Übereinstimmung mit den Experimenten zu
beobachten. Zwar wird der Verlauf qualitativ in gleicher Weise erfasst, das
Niveau unterscheidet sich jedoch deutlich. Die Ursache dafür liegt zum
einen im Experiment, wo aufgrund von 3D-Effekten und des Messverfahrens mit
Fehlern zu rechnen ist, und zum anderen im numerischen Verfahren, da die
Vorhersage von 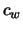 stark vom Auflösungsvermögen des wandnahen
Gitters abhängig ist [5]. Für die Anforderungen hier
ist es aber vor allem wichtig, die Verhältnisse zwischen den einzelnen
Konfigurationen richtig zu erfassen.
Von besonderem Interesse ist die aerodynamische Güte.
Sie ist als reziproke Gleitzahl definiert:
stark vom Auflösungsvermögen des wandnahen
Gitters abhängig ist [5]. Für die Anforderungen hier
ist es aber vor allem wichtig, die Verhältnisse zwischen den einzelnen
Konfigurationen richtig zu erfassen.
Von besonderem Interesse ist die aerodynamische Güte.
Sie ist als reziproke Gleitzahl definiert:
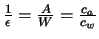 .
Ihr maximaler d.h. optimaler Wert ergibt sich
durch die Tangente vom Ursprung an die Polare.
Im Vergleich zum nackten Profil weisen die Polaren mit Gurney-Flap am HQ17
wie erwartet schlechtere aerodynamische Güten auf.
Ursache dafür ist der stark wachsende
Widerstand bei ansteigendem Auftrieb.
Im Gegensatz dazu unterscheiden sich beim NACA4412-Profil Gurneys mit
unterschiedlicher Höhe wesentlich in ihrer Güte. Der beste Werte wird
für
.
Ihr maximaler d.h. optimaler Wert ergibt sich
durch die Tangente vom Ursprung an die Polare.
Im Vergleich zum nackten Profil weisen die Polaren mit Gurney-Flap am HQ17
wie erwartet schlechtere aerodynamische Güten auf.
Ursache dafür ist der stark wachsende
Widerstand bei ansteigendem Auftrieb.
Im Gegensatz dazu unterscheiden sich beim NACA4412-Profil Gurneys mit
unterschiedlicher Höhe wesentlich in ihrer Güte. Der beste Werte wird
für 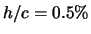 erreicht.
erreicht.
Abbildung:
Einfluss der Länge des Gurney-Flaps auf Auftrieb und
Widerstand,
links: beim HQ17; rechts: beim NACA4412.
|
|
In den Abbildungen ![[*]](crossref.png) sind die aerodynamischen Beiwerte
relativ zum jeweils korrespondierenden Beiwert des nackten Profils dargestellt.
sind die aerodynamischen Beiwerte
relativ zum jeweils korrespondierenden Beiwert des nackten Profils dargestellt.
Abbildung:
Druckverteilung bei
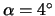 mit unterschiedlichen
Gurney-Flaps
links: beim HQ17; rechts: beim NACA4412.
mit unterschiedlichen
Gurney-Flaps
links: beim HQ17; rechts: beim NACA4412.
|
|
Wie die Druckverteilungen in Abbildung ![[*]](crossref.png) zeigen,
wird die Strömung sowohl auf der Ober- als auch auf der Unterseite des Profils
erheblich beeinflusst,
obwohl das Gurney-Flap auf der Unterseite angebracht ist.
Der größte Teil des Auftriebsgewinns entsteht auf der Profiloberseite,
die Staupunktwanderung
in Richtung Hinterkante führt hier zu einer stärker ausgeprägten
Saugspitze.
Vor dem Gurney-Flap kommt es zu einer Druckspitze, welche durch den
Druckanstieg aufgrund der Versperrung entsteht.
Diese beiden Phänomene
sorgen für den Zuwachs an Auftrieb, der bei beiden Profilen zu beobachten ist.
Im Gegensatz zu Profilen mit spitzen Hinterkanten, profitiert
der Auftrieb von dem durch das Gurney-Flap ermöglichten
Druckunterschied zwischen Ober- und Unterseite im Bereich der Hinterkante.
Der Momentenbeiwert wird infolge des Gurney-Flaps deutlich vergrößert,
wie in Tabelle
zeigen,
wird die Strömung sowohl auf der Ober- als auch auf der Unterseite des Profils
erheblich beeinflusst,
obwohl das Gurney-Flap auf der Unterseite angebracht ist.
Der größte Teil des Auftriebsgewinns entsteht auf der Profiloberseite,
die Staupunktwanderung
in Richtung Hinterkante führt hier zu einer stärker ausgeprägten
Saugspitze.
Vor dem Gurney-Flap kommt es zu einer Druckspitze, welche durch den
Druckanstieg aufgrund der Versperrung entsteht.
Diese beiden Phänomene
sorgen für den Zuwachs an Auftrieb, der bei beiden Profilen zu beobachten ist.
Im Gegensatz zu Profilen mit spitzen Hinterkanten, profitiert
der Auftrieb von dem durch das Gurney-Flap ermöglichten
Druckunterschied zwischen Ober- und Unterseite im Bereich der Hinterkante.
Der Momentenbeiwert wird infolge des Gurney-Flaps deutlich vergrößert,
wie in Tabelle ![[*]](crossref.png) zu erkennen ist.
zu erkennen ist.
Tabelle:
Dominante Frequenz und integrale Beiwerte bei
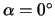 und unterschiedlich großen Gurney-Flaps
und unterschiedlich großen Gurney-Flaps
| |
| 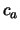 |
| 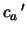 |
| 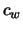 |
| 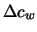 |
| 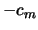 |
| 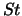 |
| |
| HQ17 |
| 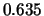 |
| 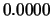 |
| 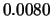 |
| |
| 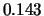 |
| 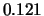 |
| |
Gurney (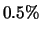 ) ) |
| 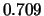 |
| 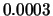 |
| 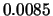 |
| 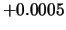 |
| 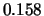 |
| 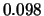 |
| |
Gurney (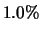 ) ) |
| 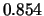 |
| 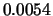 |
| 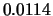 |
| 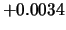 |
| 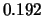 |
| 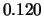 |
| |
Gurney (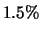 ) ) |
| 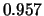 |
| 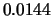 |
| 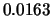 |
| 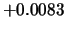 |
| 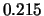 |
| 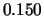 |
| |
Gurney (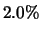 ) ) |
| 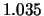 |
| 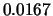 |
| 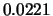 |
| 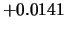 |
| 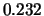 |
| 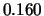 |
| |
Unterabschnitte


Nächste Seite: Instationäre Strömungsstrukturen im Nachlauf
Aufwärts: Instationäre Strömungsstrukturen im Nachlauf
Vorherige Seite: Gitter
Markus Schatz
2004-01-28
![\includegraphics[width=0.48\textwidth]{ca_flap_hq17_llr.eps}%%](img23.png)
![\includegraphics[width=0.48\textwidth]{ca_flap_naca4412_sa.eps}%%](img24.png)
![[*]](crossref.png) dargestellt. Es zeigt sich
deutlich, dass der Auftriebsbeiwert bei beiden Profilen mit der Länge des
Gurney-Flaps ansteigt. Der Gewinn an Auftrieb bleibt dabei über einen breiten
Anstellwinkelbereich (
dargestellt. Es zeigt sich
deutlich, dass der Auftriebsbeiwert bei beiden Profilen mit der Länge des
Gurney-Flaps ansteigt. Der Gewinn an Auftrieb bleibt dabei über einen breiten
Anstellwinkelbereich (
![[*]](crossref.png) ).
Diese Veränderung des Abströmwinkels und damit der Zirkulation bewirkt
potentialtheoretisch eine Veränderung des Auftriebs, wobei
ein linearer Zusammenhang zwischen Abströmwinkel und Auftrieb besteht,
während der Widerstand etwa quadratisch vom Abströmwinkel abhängt.
).
Diese Veränderung des Abströmwinkels und damit der Zirkulation bewirkt
potentialtheoretisch eine Veränderung des Auftriebs, wobei
ein linearer Zusammenhang zwischen Abströmwinkel und Auftrieb besteht,
während der Widerstand etwa quadratisch vom Abströmwinkel abhängt.
![\includegraphics[width=0.47\textwidth]{abwinkel.eps}%%](img28.png)
![\includegraphics[width=0.48\textwidth,clip]{gamma_ca_cw_hq17.eps}](img29.png)
![[*]](crossref.png) ). Dabei
fällt besonders auf, dass der relative Widerstandszuwachs bei beiden Profilen
im unteren Anstellungsbereich (
). Dabei
fällt besonders auf, dass der relative Widerstandszuwachs bei beiden Profilen
im unteren Anstellungsbereich (
![\includegraphics[width=0.48\textwidth]{ca_cw_hq17_llr.eps}%%](img33.png)
![\includegraphics[width=0.48\textwidth]{ca_cw_naca4412_sa.eps}%%](img34.png)
![\includegraphics[width=0.48\textwidth]{cacw_flap_hq17.eps}%%](img38.png)
![\includegraphics[width=0.48\textwidth]{cacw_flap_naca4412.eps}%%](img39.png)
![[*]](crossref.png) sind die aerodynamischen Beiwerte
relativ zum jeweils korrespondierenden Beiwert des nackten Profils dargestellt.
sind die aerodynamischen Beiwerte
relativ zum jeweils korrespondierenden Beiwert des nackten Profils dargestellt.
![\includegraphics[width=0.48\textwidth]{cp_04_hq17.eps}%%](img40.png)
![\includegraphics[width=0.48\textwidth]{cp_04_naca4412.eps}%%](img41.png)
![[*]](crossref.png) zeigen,
wird die Strömung sowohl auf der Ober- als auch auf der Unterseite des Profils
erheblich beeinflusst,
obwohl das Gurney-Flap auf der Unterseite angebracht ist.
Der größte Teil des Auftriebsgewinns entsteht auf der Profiloberseite,
die Staupunktwanderung
in Richtung Hinterkante führt hier zu einer stärker ausgeprägten
Saugspitze.
Vor dem Gurney-Flap kommt es zu einer Druckspitze, welche durch den
Druckanstieg aufgrund der Versperrung entsteht.
Diese beiden Phänomene
sorgen für den Zuwachs an Auftrieb, der bei beiden Profilen zu beobachten ist.
Im Gegensatz zu Profilen mit spitzen Hinterkanten, profitiert
der Auftrieb von dem durch das Gurney-Flap ermöglichten
Druckunterschied zwischen Ober- und Unterseite im Bereich der Hinterkante.
Der Momentenbeiwert wird infolge des Gurney-Flaps deutlich vergrößert,
wie in Tabelle
zeigen,
wird die Strömung sowohl auf der Ober- als auch auf der Unterseite des Profils
erheblich beeinflusst,
obwohl das Gurney-Flap auf der Unterseite angebracht ist.
Der größte Teil des Auftriebsgewinns entsteht auf der Profiloberseite,
die Staupunktwanderung
in Richtung Hinterkante führt hier zu einer stärker ausgeprägten
Saugspitze.
Vor dem Gurney-Flap kommt es zu einer Druckspitze, welche durch den
Druckanstieg aufgrund der Versperrung entsteht.
Diese beiden Phänomene
sorgen für den Zuwachs an Auftrieb, der bei beiden Profilen zu beobachten ist.
Im Gegensatz zu Profilen mit spitzen Hinterkanten, profitiert
der Auftrieb von dem durch das Gurney-Flap ermöglichten
Druckunterschied zwischen Ober- und Unterseite im Bereich der Hinterkante.
Der Momentenbeiwert wird infolge des Gurney-Flaps deutlich vergrößert,
wie in Tabelle ![[*]](crossref.png) zu erkennen ist.
zu erkennen ist.