

Nächste Seite: Modifizierte Gurney-Flaps
Aufwärts: Ergebnisse
Vorherige Seite: Instationäre Strömungsstrukturen im Nachlauf
Untersuchungen der zweidimensionalen Geometrie mit einer dreidimensionalen
Simulation ergeben, dass die Strömung im wesentlichen zweidimensional ist.
Zwar sind in den Isoflächendarstellungen der Momentanwerte von 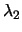 in
Abbildung
in
Abbildung ![[*]](crossref.png) leichte 3D-Effekt, insbesondere im nahen
Nachlauf der Profiloberseite, auszumachen, im wesentlichen ist jedoch
das Abschwimmen von nahezu zweidimensionalen Rollen im Nachlauf zu erkennen.
Sowohl der mittlere Auftrieb als auch die Dynamik unterscheiden sich kaum von
der zweidimensionalen Lösung.
Der Verlauf des Auftriebsbeiwerts zeigt in seinem Spektrum die typischen
Eigenschaften einer URANS-Simulation mit einem großen Abstand in der
Intensität zwischen den Frequenzspitzen
und dem Rauschen (Abb.
leichte 3D-Effekt, insbesondere im nahen
Nachlauf der Profiloberseite, auszumachen, im wesentlichen ist jedoch
das Abschwimmen von nahezu zweidimensionalen Rollen im Nachlauf zu erkennen.
Sowohl der mittlere Auftrieb als auch die Dynamik unterscheiden sich kaum von
der zweidimensionalen Lösung.
Der Verlauf des Auftriebsbeiwerts zeigt in seinem Spektrum die typischen
Eigenschaften einer URANS-Simulation mit einem großen Abstand in der
Intensität zwischen den Frequenzspitzen
und dem Rauschen (Abb. ![[*]](crossref.png) ). Im Vergleich zur
zweidimensionalen
Betrachtung tritt jedoch eine weitere Spitze bei geringen Frequenzen auf,
die durch die dreidimensionale Dynamik des Wirbelaufrollens entsteht.
Die hochauflösenden DES-Untersuchungen werden zur Zeit durchgeführt.
Als Voruntersuchung können dazu die Ergebnisse einer zweidimensionalen DES
betrachtet werden. Mit ihrer Hilfe kann bereits geprüft werden,
in welchen Bereichen das Verfahren in den URANS- bzw. LES-Modus wechselt.
Wie erwartet geschieht das vor allem im Nachlauf des Gurney-Flaps.
Der qualitative Verlauf des Auftriebs bei der zweidimensionalen DES
unterscheidet sich durch die Auflösung der turbulenten Fluktuationen
deutlich von den URANS-Ergebnissen. Im Spektrum ist hier das turbulente
Rauschen zu erkennen (Abb.
). Im Vergleich zur
zweidimensionalen
Betrachtung tritt jedoch eine weitere Spitze bei geringen Frequenzen auf,
die durch die dreidimensionale Dynamik des Wirbelaufrollens entsteht.
Die hochauflösenden DES-Untersuchungen werden zur Zeit durchgeführt.
Als Voruntersuchung können dazu die Ergebnisse einer zweidimensionalen DES
betrachtet werden. Mit ihrer Hilfe kann bereits geprüft werden,
in welchen Bereichen das Verfahren in den URANS- bzw. LES-Modus wechselt.
Wie erwartet geschieht das vor allem im Nachlauf des Gurney-Flaps.
Der qualitative Verlauf des Auftriebs bei der zweidimensionalen DES
unterscheidet sich durch die Auflösung der turbulenten Fluktuationen
deutlich von den URANS-Ergebnissen. Im Spektrum ist hier das turbulente
Rauschen zu erkennen (Abb. ![[*]](crossref.png) ).
).
Abbildung:
Darstellung von Strömungsstrukturen durch Isoflächen von
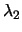 im Nachlauf,
links: eines zweidimensionalen Gurney-Flaps;
rechts: eines Gurney-Flaps mit Schlitz.
im Nachlauf,
links: eines zweidimensionalen Gurney-Flaps;
rechts: eines Gurney-Flaps mit Schlitz.
|
|
Abbildung:
links: Frequenzspektrum des Auftriebsbeiwerts im
Vergleich von
2D-URANS, 2D-DES und 3D-URANS beim HQ17-Profil mit Gurney-Flap
(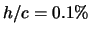 );
rechts: typische Größe der ablösenden Wirbel .
);
rechts: typische Größe der ablösenden Wirbel .
|
|


Nächste Seite: Modifizierte Gurney-Flaps
Aufwärts: Ergebnisse
Vorherige Seite: Instationäre Strömungsstrukturen im Nachlauf
Markus Schatz
2004-01-28
![\includegraphics[width=0.48\textwidth]{lam_gurney.eps}%%](img97.png)
![\includegraphics[width=0.48\textwidth]{lam_schlitz.eps}%%](img98.png)
![[*]](crossref.png) leichte 3D-Effekt, insbesondere im nahen
Nachlauf der Profiloberseite, auszumachen, im wesentlichen ist jedoch
das Abschwimmen von nahezu zweidimensionalen Rollen im Nachlauf zu erkennen.
Sowohl der mittlere Auftrieb als auch die Dynamik unterscheiden sich kaum von
der zweidimensionalen Lösung.
Der Verlauf des Auftriebsbeiwerts zeigt in seinem Spektrum die typischen
Eigenschaften einer URANS-Simulation mit einem großen Abstand in der
Intensität zwischen den Frequenzspitzen
und dem Rauschen (Abb.
leichte 3D-Effekt, insbesondere im nahen
Nachlauf der Profiloberseite, auszumachen, im wesentlichen ist jedoch
das Abschwimmen von nahezu zweidimensionalen Rollen im Nachlauf zu erkennen.
Sowohl der mittlere Auftrieb als auch die Dynamik unterscheiden sich kaum von
der zweidimensionalen Lösung.
Der Verlauf des Auftriebsbeiwerts zeigt in seinem Spektrum die typischen
Eigenschaften einer URANS-Simulation mit einem großen Abstand in der
Intensität zwischen den Frequenzspitzen
und dem Rauschen (Abb. ![[*]](crossref.png) ). Im Vergleich zur
zweidimensionalen
Betrachtung tritt jedoch eine weitere Spitze bei geringen Frequenzen auf,
die durch die dreidimensionale Dynamik des Wirbelaufrollens entsteht.
Die hochauflösenden DES-Untersuchungen werden zur Zeit durchgeführt.
Als Voruntersuchung können dazu die Ergebnisse einer zweidimensionalen DES
betrachtet werden. Mit ihrer Hilfe kann bereits geprüft werden,
in welchen Bereichen das Verfahren in den URANS- bzw. LES-Modus wechselt.
Wie erwartet geschieht das vor allem im Nachlauf des Gurney-Flaps.
Der qualitative Verlauf des Auftriebs bei der zweidimensionalen DES
unterscheidet sich durch die Auflösung der turbulenten Fluktuationen
deutlich von den URANS-Ergebnissen. Im Spektrum ist hier das turbulente
Rauschen zu erkennen (Abb.
). Im Vergleich zur
zweidimensionalen
Betrachtung tritt jedoch eine weitere Spitze bei geringen Frequenzen auf,
die durch die dreidimensionale Dynamik des Wirbelaufrollens entsteht.
Die hochauflösenden DES-Untersuchungen werden zur Zeit durchgeführt.
Als Voruntersuchung können dazu die Ergebnisse einer zweidimensionalen DES
betrachtet werden. Mit ihrer Hilfe kann bereits geprüft werden,
in welchen Bereichen das Verfahren in den URANS- bzw. LES-Modus wechselt.
Wie erwartet geschieht das vor allem im Nachlauf des Gurney-Flaps.
Der qualitative Verlauf des Auftriebs bei der zweidimensionalen DES
unterscheidet sich durch die Auflösung der turbulenten Fluktuationen
deutlich von den URANS-Ergebnissen. Im Spektrum ist hier das turbulente
Rauschen zu erkennen (Abb. ![[*]](crossref.png) ).
).
![\includegraphics[width=0.48\textwidth]{lam_gurney.eps}%%](img97.png)
![\includegraphics[width=0.48\textwidth]{lam_schlitz.eps}%%](img98.png)
![\includegraphics[width=0.48\textwidth]{spektrum_gurney.eps}%%](img99.png)
![\includegraphics[width=0.48\textwidth]{wirbelgroesse.eps}%%](img100.png)