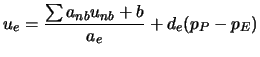 |
(6.28) |
Eine Gleichung für das Druckfeld erhalten wir wie folgt. Die Impulsgleichung (6.8) wird geschrieben als
mit ![]() nach (6.18).
Wir definieren eine Pseudo-Geschwindigkeit
nach (6.18).
Wir definieren eine Pseudo-Geschwindigkeit
![]() :
:
![]() setzt sich aus den Nachbargeschwindigkeiten
setzt sich aus den Nachbargeschwindigkeiten ![]() zusammen und
enthält keinen Druck. Gleichung (6.28) wird jetzt
zusammen und
enthält keinen Druck. Gleichung (6.28) wird jetzt
und analog
Die Analogie zwischen diesen Gleichungen und den Gleichungen
(6.19 - 6.21) ist
leicht zu sehen. Statt
![]() haben wir hier
haben wir hier
![]() und der Druck
und der Druck ![]() selbst tritt an die Stelle von
selbst tritt an die Stelle von ![]() . Aus der Herleitung in
Kapitel 6.6 folgt dann bei Verwendung dieser neuen
Geschwindigkeits-Druck-Beziehung eine Gleichung für den Druck:
. Aus der Herleitung in
Kapitel 6.6 folgt dann bei Verwendung dieser neuen
Geschwindigkeits-Druck-Beziehung eine Gleichung für den Druck:
mit ![]() usw. nach (6.25);
die Konstante
usw. nach (6.25);
die Konstante ![]() ist gegeben durch:
ist gegeben durch:
Dieser Ausdruck für ![]() ist der einzige Unterschied zwischen der
Druckgleichung (6.33) und der Druckkorrekturgleichung
(6.24). Der Ausdruck (6.34) für
ist der einzige Unterschied zwischen der
Druckgleichung (6.33) und der Druckkorrekturgleichung
(6.24). Der Ausdruck (6.34) für ![]() verwendet
die Pseudogeschwindigkeiten
verwendet
die Pseudogeschwindigkeiten
![]() , während
, während ![]() für
die
für
die ![]() -Gleichung mit den gesternten Geschwindigkeiten
berechnet wurde. Obwohl die Druckgleichung und die Druckkorrekturgleichung fast
identisch sind, besteht ein wesentlicher Unterschied: In der Herleitung der
Druckgleichung wurden keine Näherungen gemacht. Verwendet man ein korrektes
Geschwindigkeitsfeld zur Berechnung der Pseudo-Geschwindigkeiten, dann ergibt
die Druckgleichung sofort den korrekten Druck.
-Gleichung mit den gesternten Geschwindigkeiten
berechnet wurde. Obwohl die Druckgleichung und die Druckkorrekturgleichung fast
identisch sind, besteht ein wesentlicher Unterschied: In der Herleitung der
Druckgleichung wurden keine Näherungen gemacht. Verwendet man ein korrektes
Geschwindigkeitsfeld zur Berechnung der Pseudo-Geschwindigkeiten, dann ergibt
die Druckgleichung sofort den korrekten Druck.