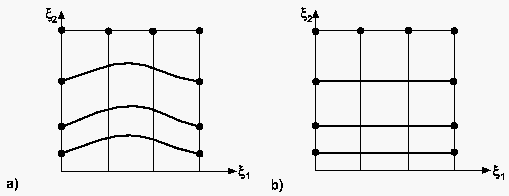
Neben der Bestimmung der Kontrollfunktion aus einem algebraischen Netz besteht eine zweite Methode darin, diese aus der Punkteverteilung auf der Berandung zu berechnen und anschließend in das Gebietsinnere zu interpolieren. Dazu wird Gleichung (6.120) auf eine Koordinatenlinie bzw. Koordinatenfläche projiziert und die resultierende Gleichung nach den Kontrollfunktionen aufgelöst. Um dies zu verdeutlichen, werden folgende einfache Beispiele betrachtet. Abbildung 82 zeigt ein physikalisches Rechteck mit ungleichförmiger Punkteverteilung auf den vertikalen Rändern (Richtung) und äquidistanter Verteilung auf den horizontalen Rändern (Richtung). Ohne die Kontrollfunktionen (d.h. ) liefert die Gleichung (6.119) ein Gitternetz, wie in Abbildung 82a dargestellt. Wünschenswert aber ist ein Koordinatenlinienverlauf, wie er in Abbildung 82b zu sehen ist.
 |
Mit den Transformationsgleichungen für die Punktekoordinaten: gilt dann:
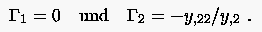 |
(6.122) |
Die Krümmungsanteile verschwinden, da die Koordinatenlinien nicht gekrümmt sein sollen. ergibt sich aufgrund der äquidistanten Punkteverteilung in Richtung zu null, wohingegen einen Anteil aus der ungleichförmigen Punkteverteilung in Richtung erhält. wird schließlich zwischen dem rechten und linken Rand ins Gebietsinnere interpoliert.
Im Falle eines O-Gitters um einen Zylinder lauten die Transformationsgleichungen: und mit . Damit ergibt sich wie im vorangegangenen Fall zu Null, erhält jetzt einen zusätzlichen Term , der sich aus einem Bogenlängenanteil und einem Krümmungsanteil zusammensetzt. Damit folgt:
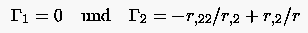 |
(6.123) |
Hier würde die Vernachlässigung des Krümmungstermes bewirken, daß sich die Koordinatenlinien stärker an die konvexe Oberfläche des Zylinders anschmiegten.
Als drittes Beispiel sei ein C-Gitter um einen Zylinder betrachtet (Abb. 83), das die Problematik der beiden vorangegangenen Fälle in sich vereinigt. So liefert die Kontrollfunktion aus Gleichung (6.122) ein adäquates Gitter für den rechten Bereich in Abbildung 82, während die Kontrollfunktion aus der Gleichung (6.123) im Bereich um den Zylinder angemessener ist. Die Konsequenz daraus ist, daß zur Bestimmung der Kontrollfunktion lediglich die Bogenlängenanteile und zwischen den vertikalen Rändern des ''computational domain'' ins Gebietsinnere interpoliert werden. Der Krümmungsanteil ist jedoch durch die Krümmung der inneren und äußeren Berandung des ''physical domain'' bestimmt, die im rechten Bereich verschwindet und um den Zylinder ihr Maximum annimmt. Darum liegt es nahe, den Krümmungsterm im Gebietsinneren durch Interpolation der entsprechenden Werte auf der unteren und oberen Berandung des Rechengebietes zu ermitteln.
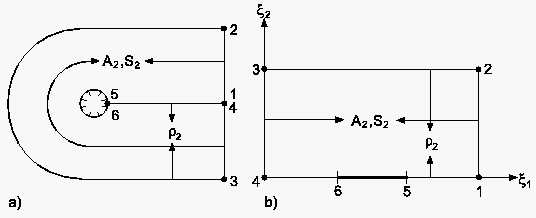 |
Abbildung 83: C-Gitter um einen Zylinder a) ''physical domain''
b) ''computational domain''