Derivativa des Rechengebiets

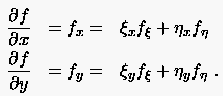
Die im vergangenen Abschnitt diskutierten Zusammenhänge zwischen den Metrikkomponenten zweier, zueinander inverser Abbildungsvorschriften ermöglichen die Darstellung der kartesischen Ableitungen im Rechengebiet als alleinige Funktion der inversen Abbildung $(x,y)$(, ).

Für die ersten kartesischen Ableitungen wiederholen wir zunächst von (6.3)

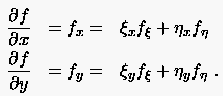(6.44)

Verwendet man anstelle der darin auftretenden Richtungsableitungen der neuen unabhängigen Veränderlichen ($$, ) nach den ursprünglichen Parametern ($x,y$) inverse Metrikkomponenten, so ergibt sich von (6.30)

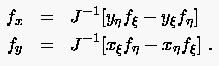(6.45)

Die Formulierung der zweiten kartesischen Ableitungen geschieht analog, z.B. für

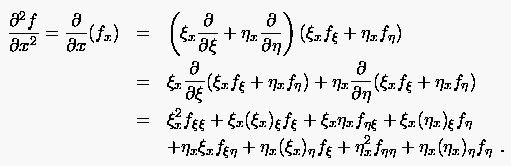(6.46)

In einem ersten Schritt ersetzt man wiederum sämtliche Metrikkomponenten durch die äquivalenten Ausdrücke auf der Basis inverser Metrikterme und erhält

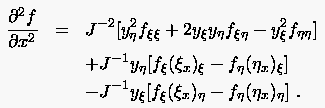(6.47)

Analog bestimmen sich die beiden anderen zweiten kartesischen Ableitungen zu

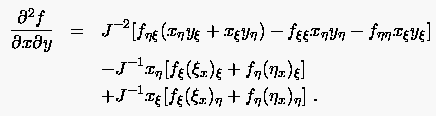(6.48)

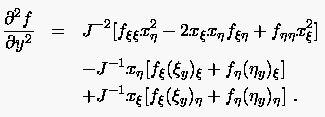(6.49)

In diesen Ausdrücken treten zusätzlich noch Ableitungen der Metrikkomponenten auf. In Kenntnis der Funktionaldeterminante ergeben sich die Beziehungen

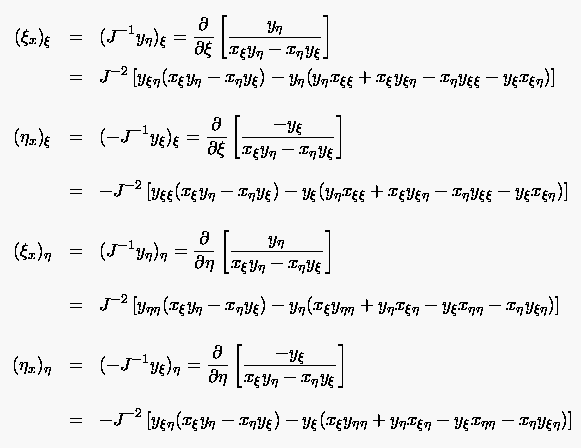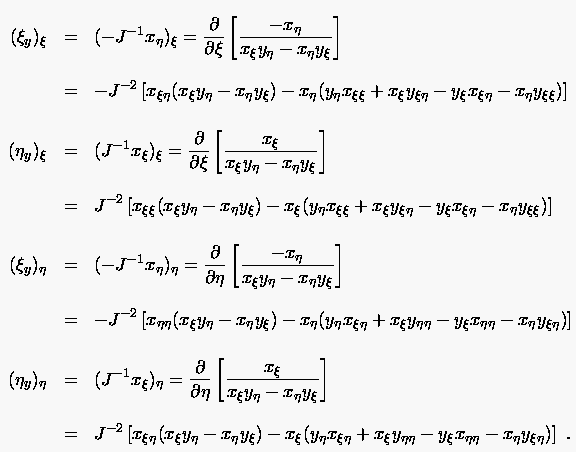	(6.50)

Aus den so gewonnenen Ausdrücken

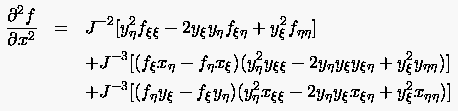(6.51)

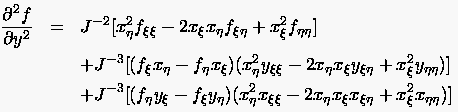(6.52)

erhält man mit Hilfe der Metrikkoeffizienten (6.33) beispielsweise die Laplacegleichung im Rechengebiet

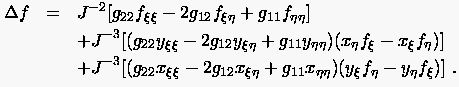(6.53)

bzw.

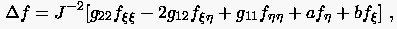(6.54)

wobei

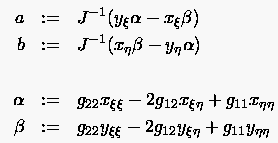(6.55)