Koordinatentransformation

 

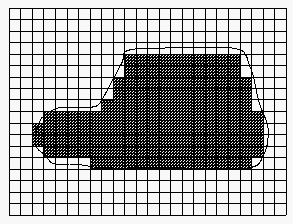
Betrachtet man anhand von Abbildung 52 sämtliche Größen bezogen auf ein kartesisches Bezugssystem, so wird deutlich, daß die Vorgabe der Randwerte für die abhängigen Variablen und deren erste Ableitungen äußerst schwierig ist. Eine beliebige Körperkontur kann vom kartesischen Gitter nur im Rahmen einer Stufenapproximation wiedergegeben werden. Für das in Abbildung 52 skizzierte Beispiel der Umströmung eines Fahrzeugs liegen sehr wenige Kontrollpunkte des kartesischen Gitters auf der Körperkontur, die die natürlichen Randbedingungen des Problems (z.B. $u,\; v=0$) beherbergt. Zur Anpassung der Lösung an die Randbedingungen bedarf es daher aufwendiger Interpolationen, die zudem stets Ungenauigkeiten mit sich führen. Daneben stellt sich die Frage, welche Werte man den abhängigen Variablen an den im Inneren des Körpers gelegenen Knotenpunten zuweist.

Abbildung 52: Stufenförmige Approximation einer Körperkontur (Fahrzeug)

Wir ziehen daraus die Schlußfolgerung, daß ein auf den Parameterlinien $x=const$ und $y=const$ des kartesischen Bezugssystems basierendes Gitter zur Beschreibung der Umströmung eines beliebigen Körpers ungeeignet ist. Demgegenüber schmiegt sich das in Abbildung 53 skizzierte körperangepaßte Gitter an den Verdrängungskörper an und ist augenscheinlich besser zur Diskretisierung der Strömungsdifferentialgleichung geeignet. Die Basis des körperangepaßten Gitters bezieht sich auf die Parameter $$ und $$ wobei die Körperkontur per Definition mit einer Parameterlinie $$= const zusammenfallen soll. Hierdurch wird ein stromlinienähnlicher Verlauf der Scharlinien $$ erzwungen. Die $($, ) Parameterlinien verlaufen im kartesischen Bezugssystem krummlinig, weshalb man vereinfacht auch von ''krummlinigen Koordinaten'' spricht. Die Scharlinien $x=const$ bzw. $y=const$ verlaufen im $($, ) Bezugssystem (Rechengebiet) jedoch nicht weniger krummlinig, wohingegen das körperangepaßte Gitter im Rechengebiet einen geradlinigen Verlauf nimmt.

Abbildung 5: Körperangepaßtes Gitter für eine Profilumströmung

In dem körperangepaßten Koordinatensystem sind die Punkte einer bestimmten Gitterlinie natürliche Randpunkte des Problems. Eine gute Auflösung der Randbedingungen durch das diskrete System ist somit gewährleistet. Für die numerische Lösung des Differentialgleichungssystems auf dem körperangepaßten Rechengitter wird die Verwendung von an kartesische Koordinaten orientierter Differenzenquotienten sehr aufwendig. Es ist daher angebracht, das ganze Problem nicht im ursprünglichen System (sog. ''physical domain''), sondern in einem körperangepaßten Rechengebiet (''computational domain'') zu betrachten. Dazu muß man die das Problem beschreibenden Differentialgleichungen in Abhängigkeit der neuen unabhängigen Veränderlichen $$ und $$ formulieren. Im folgenden sollen deshalb die Transformationsbeziehungen zwischen den beiden Sets unabhängiger Variablen hergeleitet werden.

Der Einfachheit halber betrachten wir hier nur instationäre Prozesse in den unabhängigen kartesischen Veränderlichen $x,y$ und $t$. Die Erweiterung auf räumlich dreidimensionale Probleme bereitet logisch keinerlei Schwierigkeiten. Es fallen lediglich Terme an, deren Vielzahl und Kompliziertheit häufig die Verwendung formelreduzierender Programme verlangt. Will man $(x,y,t)$ in einen anderen Variablenraum transformieren, dessen explizite Parameterdarstellung

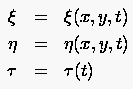(6.1)

lautet, so hat man lediglich die Kettenregel zu beachten:

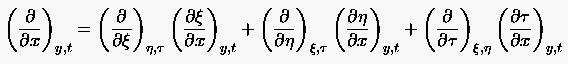(6.2)

Die Indizes der obigen Beziehung bezeichnen die bei der partiellen Ableitung festgehaltenen Variablen, werden jedoch im folgenden wieder fallengelassen. Zusammengefaßt erhält man :

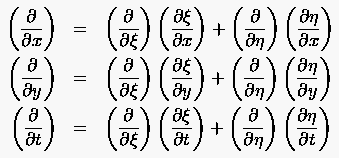(6.3)

Die Gleichungen (6.3) geben an, welche Gestalt eventuell auftretende partielle Ableitungen durch die Transformation erhalten. Die dabei auftretenden Richtungsableitungen der neuen unabhängigen Veränderlichen $($,,) nach den ursprünglichen Variablen $(x,y,t)$ wollen wir Metrikkomponenten nennen. Man bestimmt sie aus den Parameterdarstellungen (6.1). Sollten die Parameterdarstellungen geschlossene analytische Ausdrücke sein, dann lassen sich die Metrikkomponenten ebenfalls geschlossen angeben. Andernfalls sind die Metrikkomponenten numerisch z.B. durch zentrale Differenzenformeln zu bestimmen. Analog erhält man die zweiten partiellen Ableitungen

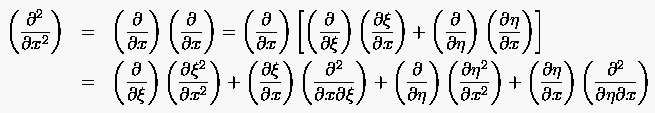(6.4)

Für die in (6.4) auftretenden gemischten Differentiationen notiert man unter erneuter Verwendung von (6.3)

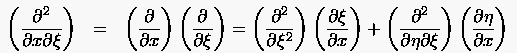(6.5)

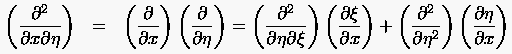(6.6)

und erhält schließlich

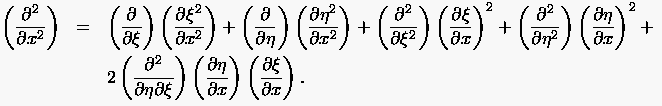(6.7)

Die Transformation der zweiten partiellen Ableitung nach $y$ ergibt

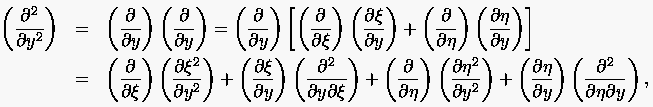(6.8)

bzw. mit

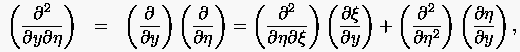(6.9)

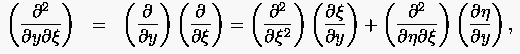(6.10)

schließlich

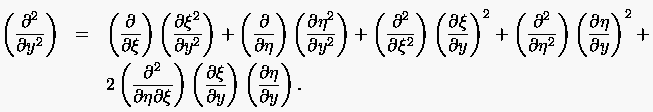(6.11)

Zum Schluß soll noch die gemischte partielle Ableitung 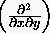transformiert werden.

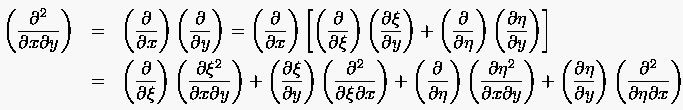(6.12)

Führt man hierin (6.5) bzw. (6.6) ein, dann ergibt sich

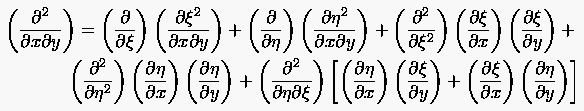(6.13)

Unangenehmerweise erhöht sich der Rechenaufwand durch die Transformation. Die transformierte Laplace Gleichung $$=0 beispielsweise lautet im $$- System

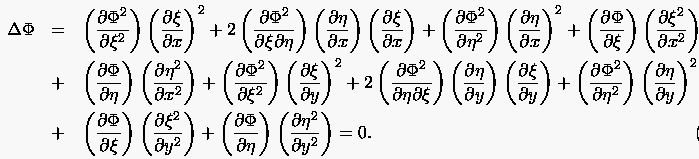(6.14)

Die Umformung von (6.14) ergibt

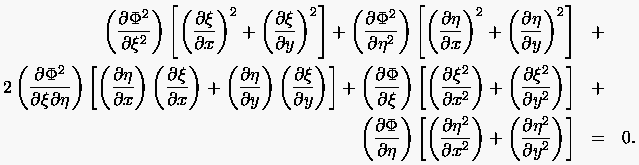(6.15)

Die o.a. Beziehnungen unterstützen die körperorientierte Diskretisierung eines ursprünglich in kartesischen Koordinaten formulierten Differentialgleichnungsproblems. Gleichung (6.1) bildet in einem ersten Schritt die bezüglich der kartesischen Basis krummlinig verlaufenden Parameternetzlinien auf ein rechtwinkeliges Rechengitter (mit einheitlichen Schrittweiten) in der $$- Ebene ab. Die darauf folgenden Gleichungen dienen zur Übertragung der das Problem beschreibenden Differentialgleichungen in das neue Bezugssystem. Die transformierten Differentialgleichungen können nun beispielsweise durch finite Differenzen in der $$- Ebene diskretisiert werden. Danach betimmt man die Werte der abhängigen Variablen an allen Gitterpunkten in der transformierten Ebene. Hierzu benutzt man einen geeigneten Lösungsalgorithmus, in dem lediglich noch die im $$- System sehr natürlich gegebenen Randbedingungen zu berücksichtigen sind. Das Ergebnis der Berechnung ist dann durch inverse Überlegungen in das Ausgangssystem übertragbar. Die nun folgenden Abschnitte beschäftigen sich mit einzelnen Abbildungsstrategien der Form (6.1). Zunächst wollen wir jedoch kurz auf die inverse Formulierung der Parameterdarstellung eingehen, die für die Eindeutigkeit der Zuordnung zwischen ''physical'' und ''computational domain'' von Bedeutung ist.

 
• Metrikkomponenten und Jakobideterminante