Wir beschränken uns auf die Diskussion der linearen partiellen Dgl. 2. Ordnung
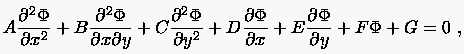 |
(1.8) |
deren Koeffizienten , , , , , , alleine Funktionen der unabhängigen Variablen sind. Es soll untersucht werden, unter welchen Umständen man mit Hilfe bekannter Lösungen zu weiteren vielleicht sogar sämtliche Lösungen eines Integrationsgebietes gelangt. Die Integration von gewöhnlichen Dgl.\ 2. Ordnung erzeugt bekanntermaßen zwei Integrationskonstanten und . Sind diese in Form von sogenannten Anfangsbedingungen an einer Stelle gegeben, so läßt sich in der Umgebung von aus der Dgl. berechnen. Es ist daher klar, daß zur Integration einer partiellen Dgl. 2. Ordnung in einer Umgebung von die drei Größen , , notwendig sind. (Mit der Anzahl der unabhängigen Veränderlichen hat sich im Vgl. zu gewöhnlichen Differentialgleichungen auch die Anzahl der Integrationsrichtungen um eins vermehrt.)
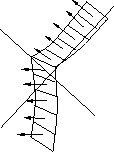
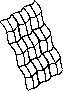
Angenommen sei die allgemeine Lösung der partiellen Differentialgleichung. Diese Lösung beschreibt eine Fläche im Variablenraum, auf der sich Raumkurven auftragen lassen (Abb. 8).

|
Einen ersten "Lösungsstreifen" 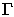 auf dieser Fläche erhält man
zu einer Kurve , an deren Punkten die drei
Größen , , gegeben sind. Der Streifen darf
natürlich keine Knicke enthalten, weswegen die Werte der partiellen
Ableitungen und über stetig ineinander übergehen
sollen.
Das bedeutet, daß auf dieser Fläche erhält man
zu einer Kurve , an deren Punkten die drei
Größen , , gegeben sind. Der Streifen darf
natürlich keine Knicke enthalten, weswegen die Werte der partiellen
Ableitungen und über stetig ineinander übergehen
sollen.
Das bedeutet, daß 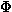 x und x und 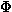 y auf stetig differenzierbar sind,
man verfügt also zusätzlich über bekannte Werte y auf stetig differenzierbar sind,
man verfügt also zusätzlich über bekannte Werte
|
|
Nach der Kettenregel sind hiermit die rechten Seiten der Gleichungen
bekannt. Die Gleichungen (1.8) bis (1.10) stellen ein lineares Gleichungssystem (1.11) zur Bestimmung der Unbekannten partiellen Ableitung 2. Ordnung dar. |
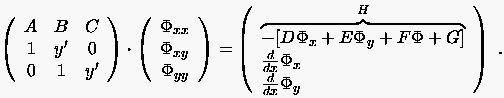 |
(1.11) |
Solch ein Gleichungssystem ist natürlich nur dann eindeutig lösbar, wenn die Determinante der Koeffizientenmatrix von null verschieden ist. Andernfalls sind die Zeilen- bzw. Spaltenvektoren dieser Matrix linear abhängig und es treten ganze Scharen von Lösungen auf.
Die Werte , ... , zu einem Punkt bestimmen ein Flächenelement 2. Ordnung zum Konvergenzpunkt
|
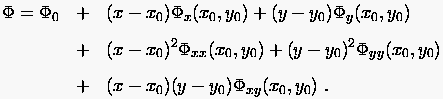
|
|
Eine noch genauere Fortsetzung der Lösung von einem Punkt  zu einem Punkt außerhalb von erhält man durch die
Taylorreihenentwicklung von . Sofern die Stetigkeit der Funktion
höherer Ordnung gegeben ist, notiert man zu einem Punkt außerhalb von erhält man durch die
Taylorreihenentwicklung von . Sofern die Stetigkeit der Funktion
höherer Ordnung gegeben ist, notiert man
|
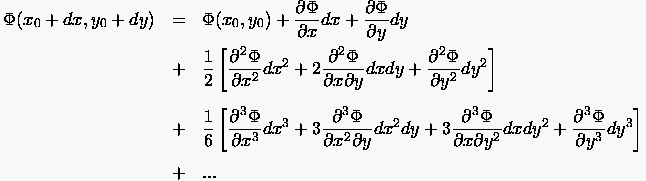
Nochmaliges partielles Ableiten nach führt beispielsweise auf das Gleichungssystem:
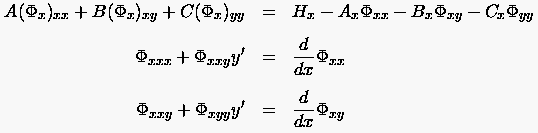
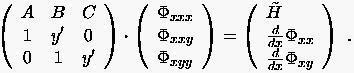 |
(1.12) |
Die Koeffizientenmatrix ist stets dieselbe. Daher reduziert sich die Aufgabe auf die Formulierung der Bedingungen, unter denen bekannte Werte , , zur Bestimmung der partiellen Ableitungen 2. Ordnung ausreichen.
Verwendet man die Cramerregel, so stellen sich die Lösungen des Gleichungssystems wie folgt dar:
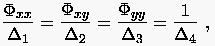 |
(1.13) |
wobei
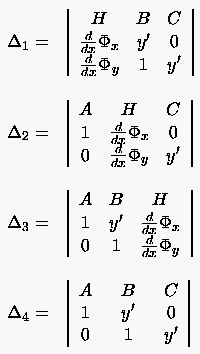
 abhängt, in der man die Lösung fortsetzen will, und für gewöhnlich in alle
Richtungen eine andere ist. Deutlich ist zu erkennen, daß sich die in einem
Punkt (etwa in Form einer Anfangsbedingung) gespeicherte Information
in alle Richtungen zur Fortsetzung der Lösung eignet. Sie breitet
sich über das gesamte Integrationsgebiet aus und erzeugt dadurch in
jedem Punkt ihren Anteil der Gesamtlösung . Die Gesamtlösung zu
einem festen Punkt aus erhält man durch Auswerten der
Superposition aller (durch Rand- und Anfangsbedingung) induzierten
Lösungsanteile an diesem Punkt. Hieraus folgt, daß eine ``unendlich lange''
Randbedingungskurve ( offenes Integrationsgebiet) unendlich
viele Lösungsanteile erzeugen würde. Eine eindeutige Lösung wäre in
keinem Punkt außerhalb der Randkurve zu ermitteln.
abhängt, in der man die Lösung fortsetzen will, und für gewöhnlich in alle
Richtungen eine andere ist. Deutlich ist zu erkennen, daß sich die in einem
Punkt (etwa in Form einer Anfangsbedingung) gespeicherte Information
in alle Richtungen zur Fortsetzung der Lösung eignet. Sie breitet
sich über das gesamte Integrationsgebiet aus und erzeugt dadurch in
jedem Punkt ihren Anteil der Gesamtlösung . Die Gesamtlösung zu
einem festen Punkt aus erhält man durch Auswerten der
Superposition aller (durch Rand- und Anfangsbedingung) induzierten
Lösungsanteile an diesem Punkt. Hieraus folgt, daß eine ``unendlich lange''
Randbedingungskurve ( offenes Integrationsgebiet) unendlich
viele Lösungsanteile erzeugen würde. Eine eindeutige Lösung wäre in
keinem Punkt außerhalb der Randkurve zu ermitteln.
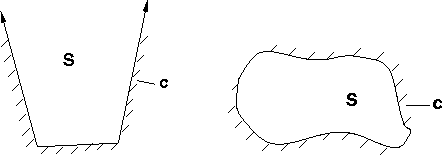
Die Existenz eindeutiger Lösungen setzt also voraus, daß sich die Orte gegebener Randbedingungen zu einer endlich langen somit geschlossenen Kurve aufreihen. Die in Kapitel 1.2 besprochenen Gleichgewichtsprobleme werden also durch elliptische Dgl. wiedergegeben.
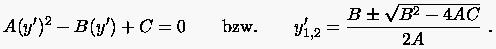 |
(1.14) |
In Abhängigkeit des Wurzelarguments heißt eine partielle Differentialgleichung:
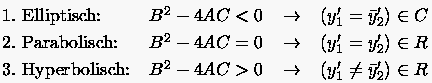
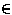 R, für die die Koeffizientendeterminante aus
(1.11) den Wert null annimmt.
R, für die die Koeffizientendeterminante aus
(1.11) den Wert null annimmt.
Dringt man von irgendeinem Punkt auf aus in dieser Richtung in das Integrationsgebiet ein, so ist das Gleichungssystem (1.11) nicht mehr eindeutig lösbar. Eventuelle mehrdeutige Lösungen sind an Nullstellen aller Zählerdeterminanten nach (1.13) gebunden. Hierbei genügt es, die Nullstellen von nur einer weiteren Determinante aufzusuchen.
 4 = 0 ist gleichbedeutend mit der linearen Abhängigkeit der
Spaltenvektoren.
4 = 0 ist gleichbedeutend mit der linearen Abhängigkeit der
Spaltenvektoren.
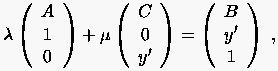
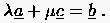
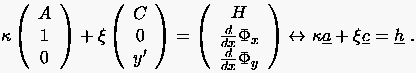
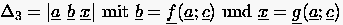
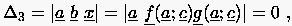
Wir wollen das von uns gewählte Beispiel 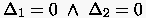 genauer ausführen. Hierzu lösen wir zunächst das Gleichungssystem (1.11) auf:
genauer ausführen. Hierzu lösen wir zunächst das Gleichungssystem (1.11) auf:
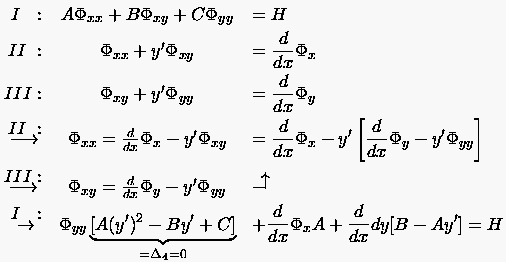
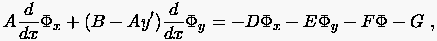 |
(1.15) |
sowie aus
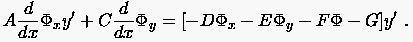 |
(1.16) |
Das Gls. (1.17) enthält keine weiteren Unbekannten, da sämtliche
Glieder über dem Bereichsrand bekannt sind (s.o.). Um einen Widerspruch
zu vermeiden, müssen (1.15) und (1.16) identisch erfüllt sein.
Der Beweis ist leicht. Man führt zunächst formal die beiden Unbekannten 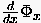 und
und 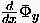 ein und notiert (1.17)
vektoriell.
ein und notiert (1.17)
vektoriell.
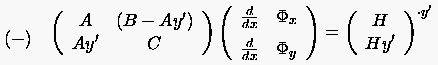 |
(1.17) |
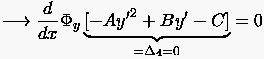
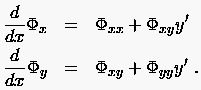
 y'2 zwei verschiedene Lösungen.
y'2 zwei verschiedene Lösungen.
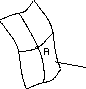
Man erhält somit von einem Punkt auf aus zwei Clusterketten (Abb. 9), die in das Integrationsgebiet eindringen; eine in Richtung , die zweite in Richtung . In der Praxis benutzen wir die Gesetzmäßigkeit, wonach sich Information entlang der Charakteristiken ausbreitet, zur Fortsetzung einer Lösung.
Da sich typengleiche Charakteristiken nicht schneiden, typenverschiedene jedoch einen Schnittpunkt besitzen, sind zur Bestimmung der Lösung im Punkte lediglich die beiden dort zur Deckung kommenden Cluster zu überlagern (siehe auch Kapitel 1.2). Sollte die Kurve, auf der die Anfangswerte gegeben sind, selbst eine Charakteristik sein, ist die Lösung nur über selbst eindeutig. In diesem Falle läßt sich zu den gegebenen Anfangswerten kein ``Informationsschnittpunkt'' finden.
Es ist sinnvoller, die mathematische Klassifizierung einer PDG direkt
auf die unabhängigen Variablen zu beziehen. Die Impulsgleichungen der
ebenen Grenzschicht (1.6) beschreiben ein Ausbreitungsproblem von
parabolischem Typ. Ihre Charakteristiken verlaufen entlang der Linien
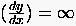 senkrecht zur Hauptströmungsrichtung.
senkrecht zur Hauptströmungsrichtung.
Der Grenzschichtaußenrand ist Anfangs- und Randbedingungskurve zugleich, die Plattenfläche ist dagegen nur Randbedingungskurve.
Das Geschwindigkeitsprofil an einer Stelle berechnet sich aus den
Anfangswerten in den stromaufliegenden Punkten 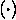 auf dem
Grenzschichtaußenrand und den Randbedingungen
auf dem
Grenzschichtaußenrand und den Randbedingungen  quer zur
Hauptströmungsrichtung. Die hieran anschließenden Profile haben keinen
Einfluß. Die Lösung pflanzt sich in Hauptströmungsrichtung vom
GS-Außenrand beginnend senkrecht zu den charakteristischen Linien zu
stromabliegenden Profilen fort. Man bezeichnet auch als die
einseitig gerichtete Koordinate des Problems. Eine Störung in
erreicht das Geschwindigkeitsprofil zu im Punkt und breitet sich
von dort aus entlang der zweiseitig gerichteten Koordinate über
das ganze Profil aus. Präziser formuliert ist die DGL parabolisch in
Richtung der Hauptströmungskoordinate und elliptisch in Richtung
der Querkoordinate .
quer zur
Hauptströmungsrichtung. Die hieran anschließenden Profile haben keinen
Einfluß. Die Lösung pflanzt sich in Hauptströmungsrichtung vom
GS-Außenrand beginnend senkrecht zu den charakteristischen Linien zu
stromabliegenden Profilen fort. Man bezeichnet auch als die
einseitig gerichtete Koordinate des Problems. Eine Störung in
erreicht das Geschwindigkeitsprofil zu im Punkt und breitet sich
von dort aus entlang der zweiseitig gerichteten Koordinate über
das ganze Profil aus. Präziser formuliert ist die DGL parabolisch in
Richtung der Hauptströmungskoordinate und elliptisch in Richtung
der Querkoordinate .
Die Zeit ist immer eine einseitig gerichtete Variable, zukünftige
Ereignisse vermögen gegenwärtige nicht mehr zu beeinflussen. Eine
einseitig gerichtete Raumkoordinate erscheint zunächst unsinnig. Mit ihr
ließen sich zwar die einseitig gerichteten konvektiven Prozesse beschreiben,
nicht jedoch diffusive Prozesse, da diese a priori zweiseitig gerichtet
sind. Wir erinnern daran, daß die Glg. (1.6) nicht die vollständige
Impulsbilanz wiedergibt, sondern nur eine Näherung, deren Güte mit wachsender
Reynoldszahl steigt. In diesem Fall spielen nach dem Grenzschichtkonzept
sämtliche Zähigkeitskräfte mit Ausnahmen von 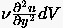 eine untergeordnete Rolle, weshalb die
Hauptströmungskoordinate zur einseitig gerichteten Koordinate wird.
Die Strategie einer sich von den Anfangswerten der Geschwindigkeit am
GS-Außenrand entlang der einseitig gerichteten Koordinate ausbreitenden
Lösung scheitert jedoch offensichtlich für Grenzschichten mit Ablösung.
eine untergeordnete Rolle, weshalb die
Hauptströmungskoordinate zur einseitig gerichteten Koordinate wird.
Die Strategie einer sich von den Anfangswerten der Geschwindigkeit am
GS-Außenrand entlang der einseitig gerichteten Koordinate ausbreitenden
Lösung scheitert jedoch offensichtlich für Grenzschichten mit Ablösung.
Es treten partielle Rückströmgebiete im wandnahen Bereich auf, womit ein derartiges Profil gewissermaßen zwei Hauptströmungsrichtungen besitzt.