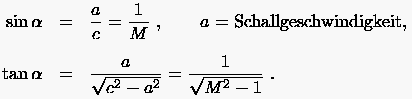Next: Mathematische Klassifizierung PDG
Up: Klassifizierung partieller Differentialgleichungen (PDG)
Previous: Lineare und nichtlineare PDG
Hinsichtlich der physikalischen Klassifizierung unterscheidet man zwischen
Gleichgewichts- und Ausbreitungsproblemen.
Gleichgewichtsprobleme hängen im allgemeinen mit der Beschreibung
stationärer Zustände zusammen. Anhand einer stationär strömenden
inkompressiblen Flüssigkeit wollen wir die Zusammenhänge von physikalischer
(Gleichgewichtsproblem) und mathematischer Gestalt (Integrationsbedingungstyp)
kurz benennen. Für verschwindend geringe Zähigkeit läßt sich der
Bewegungszustand einer solchen Flüssigkeit aus dem Gradienten eines
Geschwindigkeitspotentials ermitteln.
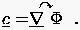 |
(1.2) |
Eine solche Strömung muß selbstverständlich auch den klassischen
Erhaltungssätzen, wie etwa dem Satz von der Erhaltung der
Masse genügen. Dieser lautet in seiner
Feldgleichungsformulierung
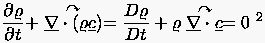 |
(1.3) |
also im hier betrachteten Fall eines inkompressiblen Mediums
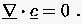 |
(1.4) |
Die Gleichungen (1.4) und (1.2) ergeben schließlich eine
partielle Differentialgleichung 2. Ordnung für die abhängige Variable
, die sog. Laplace-Gleichung
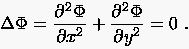 |
(1.5) |
Es handelt sich dabei immer noch um eine, wenn auch spezielle Form
des Massenerhaltungssatzes. Hiernach ruft die in der Zeiteinheit durch
die gerichtete geschlossene Oberfläche eines Kontrollvolumens
abfließende Masse 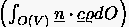 eine entsprechende Massenverminderung
eine entsprechende Massenverminderung 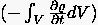 innerhalb der Bereichsgrenzen hervor.
innerhalb der Bereichsgrenzen hervor.
Für inkompressible Medien verschwinden die Glieder veränderlicher Dichte.
Deshalb ist der Zustand einer solchen Flüssigkeit beim Eintritt in
irgendein vorgegebenes Integrationsgebiet der gleiche wie beim Verlassen
des Gebietes. Da man aber letztlich vor der Aufgabe steht, die
physikalischen Verhältnisse innerhalb eines Gebietes
vorherzusagen, muß man für die Lösbarkeit dieser Aufgabe in
umgekehrter Weise folgern: Die innerhalb eines Gebietes ablaufenden
Prozesse werden eindeutiger Weise dadurch festgelegt, daß sie den
Geschehnissen entlang der Berandung das Gleichgewicht halten.
Gleichgewichtsprobleme sind im mathematischen Sinne also Randwertprobleme.
Lösungsversuche ohne die vollständige Kenntnis der Berandung wären
sinnlos, da diese ja der Formulierung des Problems bereits zu Grunde
liegen. Die Lösung ist eine Funktion der beiden unabhängigen
Veränderlichen und , bezieht sich aber nur auf Variablenkombinationen,
welche innerhalb einer ebenen geschlossenen Kurve ``'' liegen. Mit
bezeichnet man die Kurve der Randwerte, die zur eindeutigen Bestimmung
der Lösung dienen. Handelt es sich um einen mehrfach
zusammenhängenden Bereich , wie dies z.B. bei einer Profilumströmung
gegeben ist, erweitert sich die Kurve um alle inneren
Ränder.
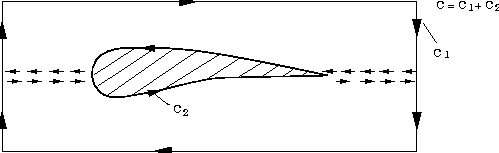
Abbildung 1:
Ausbreitungsprobleme behandeln oftmals Aufgaben, die die Zeit
als unabhängige Veränderliche enthalten. Die eindimensionale
Wellengleichung
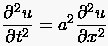
ist ein bekanntes Ausbreitungsproblem. Daneben existieren gerade in der
Thermo- und Fluiddynamik Ausbreitungsprobleme, die sich zeitlich
unabhängig (stationär) verhalten. Hierzu zählen die
Impulsgleichung der ebenen Grenzschicht
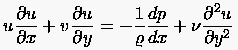 |
(1.6) |
sowie die linearisierte ebene Potentialgleichung der Gasdynamik
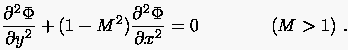
Letztere geht für (inkompressible Medien) in die Gleichung
(1.5), also in ein Gleichgewichtsproblem über.
Herausragendes Merkmal der Ausbreitungsprobleme ist die Existens von
Anfangswerten. Hiermit sind diejenigen Werte der abhängigen Variablen
gemeint, welche den physikalischen Prozeß einleiten, beispielsweise
die anfängliche Temperaturverteilung eines schlanken Stabes vor dem
Wasserbad. Die Lösung breitet sich ausgehend von den
Anfangswerten (unter Beachtung der Randbedingungen) schrittweise aus.
Welche Richtung dabei in der Ebene der unabhängigen Veränderlichen
eingeschlagen werden muß, läßt sich errechnen.
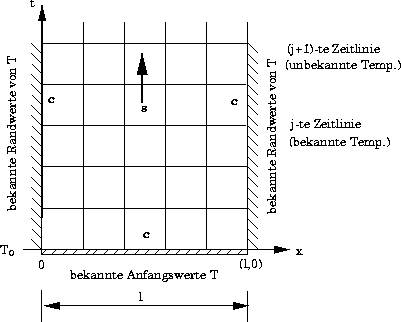
Abbildung 2:
Das Integrationsgebiet ist also offen. Im skizzierten Falle (Abb.
2) der Temperaturverteilung des schlanken Stabes
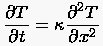
fällt die Ausbreitungsrichtung trivialer Weise mit der Zeitachse
zusammen. Die Richtungen, in der sich die Lösungen fortsetzen,
heißen charakteristische Richtungen. Sie vermögen nicht die bereits
errechneten Lösungen zu rückwertigen Stellen (nachträglich) zu
beeinflussen. Wir wollen dies am Beispiel der linearisierten ebenen
Potentialgleichung der Gasdynamik illustrieren.
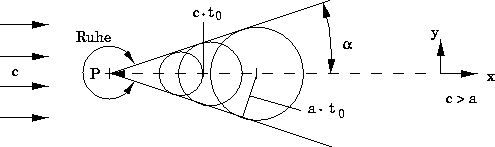
Abbildung 3:
Abb. 3 zeigt die Ausbreitung einer schwachen Störung bei einer
punktförmigen Schallquelle, die sich mit konstanter
Überschallgeschwindigkeit 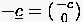 bewegt. Der Vorgang
ist (leider) instationär. Zur Zeit , an dem die Schallquelle den Punkt
erreicht hat, liegen alle früher ausgesandten Signale innerhalb des
sogenannten Machschen Kegels. Dieser ist das Einflußgebiet der
Störung.
bewegt. Der Vorgang
ist (leider) instationär. Zur Zeit , an dem die Schallquelle den Punkt
erreicht hat, liegen alle früher ausgesandten Signale innerhalb des
sogenannten Machschen Kegels. Dieser ist das Einflußgebiet der
Störung.
Außerhalb herrscht Ruhe. Für den Machwinkel 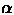 gilt:
gilt:
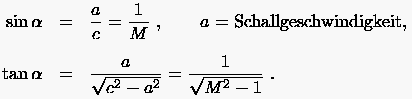
Um zu einer stationären Strömung zu gelangen, wird die Geschwindigkeit
überlagert. Das Medium strömt nun mit stationär auf
die Störquelle zu. An der Skizzierung des Problems ändert sich dadurch
nichts. Störungen können sich nur im Innern des stromab geöffneten
Machkegels im
sogenannten Abhängigkeitsgebiet
bemerkbar machen.
Das ebene Geschwindigkeitsfeld setzt sich zusammen aus der
Anströmgeschwindigkeit
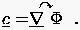
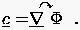
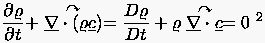
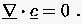
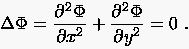
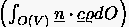 eine entsprechende Massenverminderung
eine entsprechende Massenverminderung 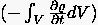 innerhalb der Bereichsgrenzen hervor.
innerhalb der Bereichsgrenzen hervor.
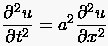
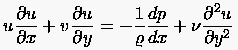
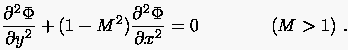
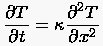
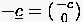 bewegt. Der Vorgang
ist (leider) instationär. Zur Zeit , an dem die Schallquelle den Punkt
erreicht hat, liegen alle früher ausgesandten Signale innerhalb des
sogenannten Machschen Kegels. Dieser ist das Einflußgebiet der
Störung.
bewegt. Der Vorgang
ist (leider) instationär. Zur Zeit , an dem die Schallquelle den Punkt
erreicht hat, liegen alle früher ausgesandten Signale innerhalb des
sogenannten Machschen Kegels. Dieser ist das Einflußgebiet der
Störung.
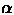 gilt:
gilt: