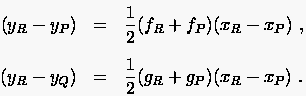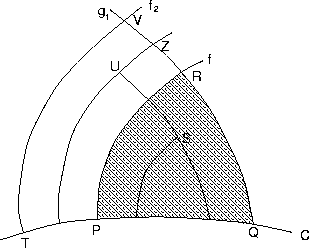
Abbildung 14:
Vorausgesetzt die Glg. (1.8) sei hyperbolisch, so sind die Wurzeln der Glg. (1.14) reel und verschieden. Wir wollen diese Wurzeln in Zukunft mit und abkürzen. Die Kurve sei eine nicht charakteristische Kurve, auf der Anfangswerte für , und bekannt sind.
Sind und zwei verschiedene Punkte von , so soll die -Charakteristik durch die -Charakteristik durch in schneiden. Da sich nirgends zwei Charakteristiken von ein und dem selben Typ schneiden, wird die Lösung in einem Punkt , der innerhalb des Dreiecks liegt, durch die Anfangsbedingungen in den Punkten und festgelegt. Analog bestimmt sich die Lösung an einem Zwischenpunkt innerhalb des Streifens aus der Anfangsbedingung in einem Punkt auf dem Bogen (die sich entlang einer -Charakteristik ausbreitet) und der Anfangsbedingung in einem Punkt auf dem Bogen (die sich auf einer -Charakteristik ausbreitet). Wenn sich die Anfangsbedingungen auf von unterscheiden, dann ist die Lösung in dem Streifen verschieden von der Lösung innerhalb des Kurvendreiecks . Strebt gegen , so geht der Streifen in die Charakteristik über. Die Unstetigkeit in den Anfangsbedingungen bei pflanzt sich also längs einer Charakteristik fort. Die Charakteristik vermag verschiedene Lösungen özu trennen. Eine äußerst wichtige Eigenart von zweiter Ordnung besteht darin, daß beide Lösungen zusammen mit ihren ersten Ableitungen stetig sein können, wohingegen die Ableitungen zweiter und höherer Ordnung dieselbe Charakteristik unstetig überschreiten. Das ist leicht einzusehen, wenn man bedenkt, daß entlang der Charakteristiken eine der partiellen Ableitungen 2. Ordnung frei wählbar war.
Wir wollen nun versuchen, einen ungefähren Wert für im unbekannten Charakteristikenschnittpunkt zu ermitteln. In erster Näherung können wir die Bögen und als Geraden mit den Steigungen und ansehen. Dann läßt sich die Änderung der -Koordinate beim Übergang zum Punkt näherungsweise durch
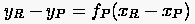 |
(1.18) |
bzw.
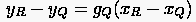 |
(1.19) |
bestimmen.
Aus den Gleichungen (1.18) und (1.19) erhält man zunächst die unbekannten Koordinaten des neuen Punktes.
Aus (1.16)
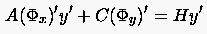
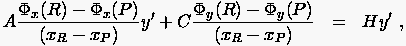 |
(1.20) |
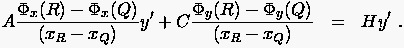 |
(1.21) |
Dies sind zwei Gleichungen für die beiden Unbekannten und . Bricht man die Taylorentwicklung nach dem ersten Glied ab, so erhält man:
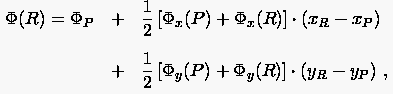 |
(1.22) |
wobei die Gradienten durch ihre Mittelwerte ersetzt wurden.
Die Approximation läßt sich verbessern, indem man in den Gleichungen (1.18) und (1.19) eine gemittelte Steigung verwendet. Die Gleichungen für verbesserte Werte und lauten dann: