Lineare und nichtlineare PDG

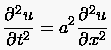
Differentialgleichungen können in lineare und nichtlineare gegliedert werden. Bei einer linearen Differentialgleichung tritt die abhängige Variable und ihre Ableitung nur linear auf, Produkte zwischen ihr und/oder ihren Ableitungen sind also ausgeschlossen. Für diesen Typ gilt das Überlagerungsprinzip, wonach sich zwei Lösungen der homogenen Ausgangsgleichung zu einer dritten superponieren lassen.

Die eindimensionale Wellengleichung

ist beispielsweise eine lineare Differentialgleichung.

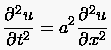
Demgegenüber enthält eine nichtlineare Differentialgleichung Produkte der abhängigen Variablen und/oder ihrer Ableitungen. Ein Beispiel ist die reibungsfreie Burgers Gleichung

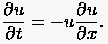
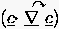Zu den nichtlinearen Differentialgleichungen zählt beispielsweise auch die Navier-Stokes-Gleichung, deren konvektiver Anteil die nichtlinearen Glieder 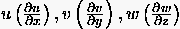enthält. Manche Lösungsstrategien lassen innerhalb der nichtlinearen auch die sog. quasilinearen Dgl. zu. Hierunter versteht man i.a. Linearität bezüglich der höchsten Ableitung (was für die N-S Gleichung zutrifft).