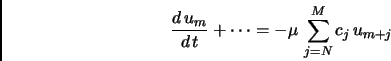Artificial Damping and Filtering

Analysis of the discrete governing equations shows that only a limited region of wavenumbers is resolved accurately. Signals of frequencies not resolved by the stencil (theoretical limit at approx. 5.4 points per wavelength) excite spurious waves that are not solutions of the original physical problem. These artifacts lead to instabilities and must be eliminated by filtering or damping.

Artificial Damping

The idea of artificial damping is based on the addition of a damping term to the governing equations. This technique is described in detail by Tam et al. (1993). Adding the damping term to the momentum equation yields for example:

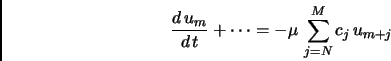$$\frac{d u_m}{d t} + \cdots = -\mu \sum^M_{j=N} c_j u_{m+j}$$ (2)

The coefficients c_j define the frequency characteristic of the damping term. They are chosen so that the damping is nearly zero for long waves, but positive and finite in the range of higher wave numbers. The advantage of the method lies in the low computational effort. Only one additional term has to be computed.

Filtering

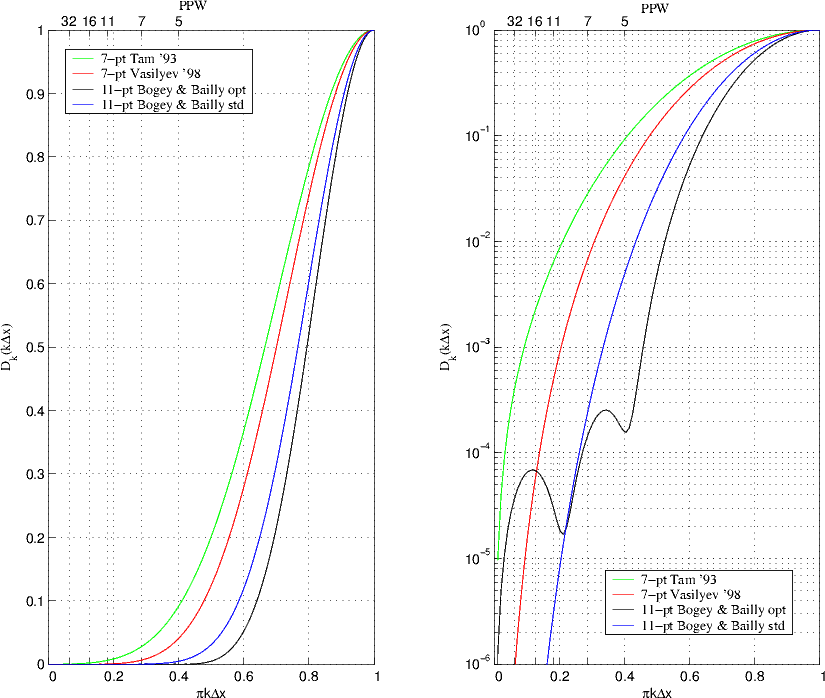
This method is independent of the governing equations. The variable field is filtered after each time integration (or in intervals) by a FIR-filter. The filter coefficients are chosen as in the case of the artificial damping to remove the high frequency components while preserving the physical solution. Filters of different point number and frequency response are shown in the diagram below.

Practice

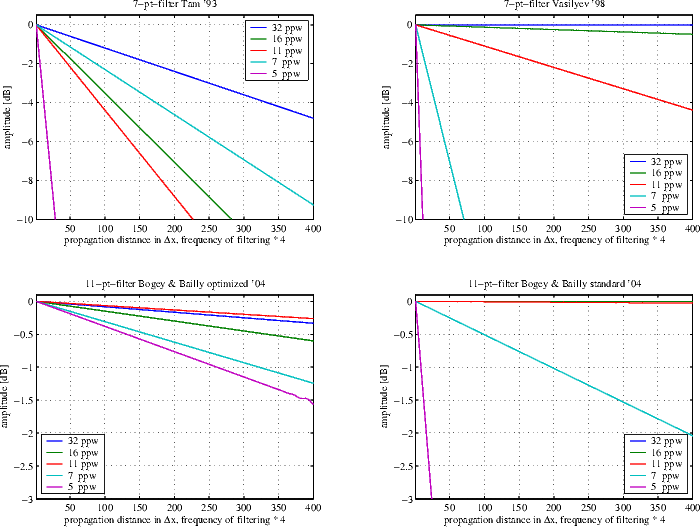
The negative aspect of damping and filtering is the attenuation of the physical solution, which arises due to the non-zero damping factor in the long wave and especially the transition range. Through the accumulation of this effect over hundreds of filter operations, the influence on the solution is not negligible. To achieve simultaneously a high slope of the filter characteristic in the transition band and a small influence on the solution, filters of high order should be used. Filters with 11 points turned out to be sufficient in practice. The influence of filtering for different wavenumbers was studied in (Panek, 2004). The results are shown in the folowing figure.

Experiments have shown that even with strong artificial damping, instabilities can occur. For this reason this technique was dropped in favour of filtering.