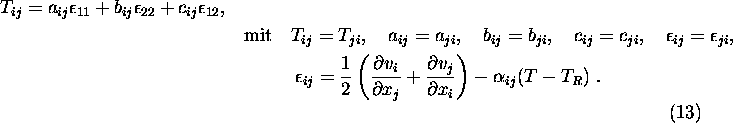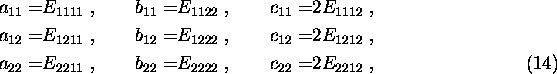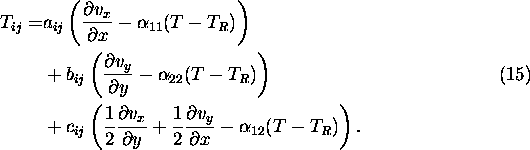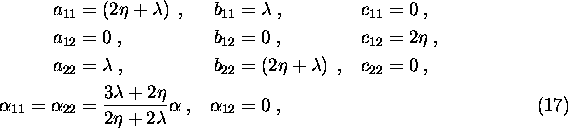Materialgesetz und Verschiebungs-Verzerrungs-Relationen

  Die Darstellung des Spannungstensors $$T im zweidimensionalen Raum ist unter Verwendung des Hookeschen Materialgesetzes mit den linearen Verschiebungs-Verzerrungs- Relationen in kartesischen Kooardinaten in Abhängigkeit der Verschiebungen sehr einfach wie folgt möglich:
 
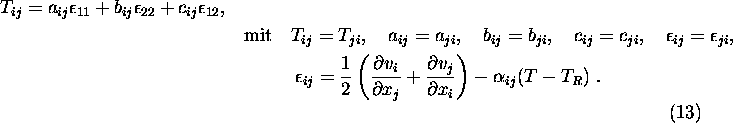
Hierbei stellen die $v$_i die Verschiebungen und die $\epsilon$_ij die (linearen) Verzerrungen dar. Mit der Temperaturdifferenz $T-T$_R wird mittels der Ausdehnungsbeiwerte $\alpha$_ij den Verzerrungen infolge einer Abweichung von der Referenztemperatur $T$_R Rechnung getragen. Diese Darstellung ist im zweidimensionalen Raum äquivalent zu

$$T=E {( D-α(T-T_R) }&thicksp;,

wenn man vereinbart, daß

$D$_ij={12} {( {&pd;v_i&pd;x_j} +{&pd;v_j&pd;x_i} }&thicksp;,

und die Konstanten wie folgt einführt:

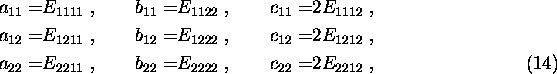
also

$E$_ijkl mit {{ ij $von$ $\{\{a$_ij b_ij c_ij $\}$ kl= $\{\{11$ für\; a$$_ij 22 $für\; b$_ij 12 $für\; c$_ij $\}$ } .

In kartesichen Koordinaten im zweidimensionalen Raum gilt dann für $i$ und $j\; =\; x,y$ oder $1,2$ folgender Zusammenhang:
 
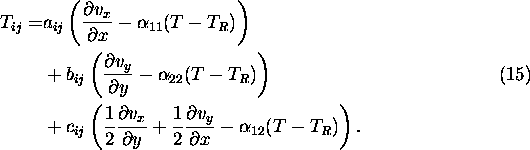
Für den Sonderfall der Isotropie wird häufig folgende Darstellung im dreidimensionlen Raum angegeben, z.B. [3] Seite 290 und [15, 16]:

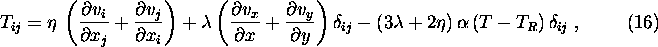
die als Sonderfall in der oben angegebenen Darstellung enthalten ist, wenn man auf zwei Dimensionen reduziert und setzt:

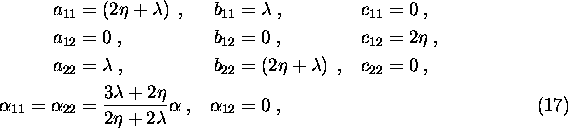
wie leicht überprüft werden kann. Über die Spannungen und Verzerrungen, die den Index 3 oder $z$ enthalten, ist keine Aussage gemacht worden!
Um das Materialgesetz der Scheibe (ebener Spannungszustand) zu erhalten, muß man fordern , daß die Spannung aus der Scheibenebene heraus Null ist. Alle Zustandsgrößen müssen sich in Abhängigkeit von zwei Koordinaten ausdrücken lassen. (Bei linearer Rechnung ist eine konstante Spannung aus der Ebene heraus damit gleichbedeutend, diese Spannung zu Null zu setzen, da sich nur ein konstanter additiver Anteil aus dieser Spannung bei der folgenden Umformung ergibt, der als Belastung behandelt werden oder über je nach Belastung scheinbar weichere oder steifere Materialkonstanten berücksichtigt werden kann.) Dies führt dann zu einfachereren Konstanten als oben angegeben. Setzt man $z=3$ als Richtung aus der Scheibenebene heraus, so wird das isotrope Elastizitätsgesetz der Scheibe zu:
 
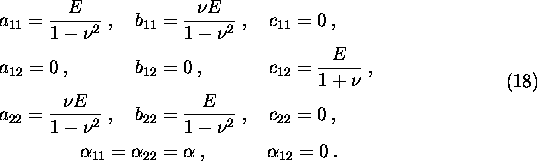
Ausgangspunkt für diesen Rechengang ist das isotrope Hooke'sche Elastizitätsgesetz:


 
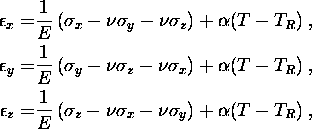
Mit der Forderung $\sigma$_z=0 und durch Inversion (Spannungen als Funktion der $\epsilon$_ij ausgedrückt) erhält man den Zusammenhang 62. Voraussetzungen zur Anwendbarkeit der Scheibentheorie mit dem oben angegebenen Materialgesetz sind eine ebene, scheibenartige Geometrie und Belastungen nur in der Neutralebene dieser Scheibe. Es gilt

wobi $E$ der isotrope Elastizitätsmodul, $G$ der Schubmodul und $\nu$ die Querkontraktionszahl sind. Dies ist identisch auch [5] auf Seite 27 und 33 zu entnehmen.

Die allgemeine Formulierung beinhaltet ebenso die Grenzfälle des ebenen Spannungszustandes und des ebenen Verzerrungszstandes. Die Koeffizienten $a$_ij, $b$_ij und $c$_ij sind mit den entsprechenden Bedingungen zu modifizieren. Dies ist allgemein möglich, da die Spannungen $T$_ij über diese Koeffizienten mit jeder Verzerrung $\epsilon$_ij voneinander unabhängig verknüpft sind, so daß praktisch jedes Materialgesetz in 59 implementierbar ist.
Für den Wärmefluß $$q wird die Gültigkeit des Fourierschen Wärmeleitungsgesetzes in etwas abgeänderter Form angesetzt:

$q$_i= λ_i   {&pd;T&pd;x_i} &thicksp;.

Mit $\lambda$_i wird eine richtungsabhängige Wärmeleitfähigkeit implementiert.