Bis jetzt wurde ein kartesisches Koordinatensystem
vorausgesetzt. Die Methode ist jedoch auf alle orthogonalen
Koordinatensysteme, z.B. Polar-Koordinaten
![]() anwendbar. Das Gegenstück zu (4.39) ist hier:
anwendbar. Das Gegenstück zu (4.39) ist hier:
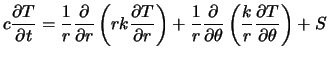 |
(4.53) |
Die z-Dicke ist 1. Die Diskretisierungsgleichung erhält man
durch Multiplikation mit
![]() und Integration über
und Integration über ![]() und
und ![]() über das Kontrollvolumen (ergibt
ein Volumenintegral, denn
über das Kontrollvolumen (ergibt
ein Volumenintegral, denn
![]() ergibt Volumenelemente mit Dicke 1). Mit
dem Vorgehen von Kapitel 4.7 erhalten wir die
Diskretisierungsgleichung:
ergibt Volumenelemente mit Dicke 1). Mit
dem Vorgehen von Kapitel 4.7 erhalten wir die
Diskretisierungsgleichung:
| (4.54) |
mit
 |
|||
 |
|||
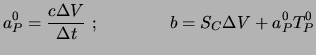 |
(4.55) |
![]() ist das Volumen des Kontrollvolumens:
ist das Volumen des Kontrollvolumens:
![]() (
(![]() ist nicht
notwendigerweise gleich
ist nicht
notwendigerweise gleich
![]() , außer wenn
, außer wenn ![]() in der
Mitte zwischen
in der
Mitte zwischen ![]() und
und ![]() liegt; Praxis B).
liegt; Praxis B).