| (4.37) |
Unter Einschluß des Quellterms ergibt sich
mit
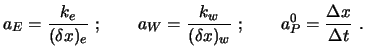 |
Für
![]() ergibt sich die
stationäre Diskretisierungsgleichung (4.2/4.3).
ergibt sich die
stationäre Diskretisierungsgleichung (4.2/4.3).
Wichtigstes Prinzip des voll impliziten Schemas ist die
Gültigkeit des neuen Wertes von ![]() über den ganzen Zeitschritt.
Ist
über den ganzen Zeitschritt.
Ist ![]() temperaturabhängig, muß es iterativ aus
temperaturabhängig, muß es iterativ aus ![]() berechnet
werden, genau wie im stationären Verfahren.
berechnet
werden, genau wie im stationären Verfahren.
Andere Aspekte des
stationären Verfahrens gelten genauso im instationären Fall:
Randbedingungen, Quellterm-Linearisierung, TDMA.
Die Erweiterung auf 2
und 3 Dimensionen ist einfach, wie im folgenden Kapitel gezeigt wird.