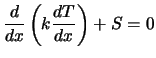 |
(4.1) |
Das Beispiel in Kapitel 3 war ein Vehikel zur
Erläuterung der vier Grundregeln, gleichzeitig wurde dort bereits
alles abgeleitet. Deshalb hier nur eine kurze
Zusammenfassung:
Die Grundgleichung
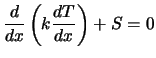 |
(4.1) |
führt auf die Diskretisierungsgleichung
worin
Die Kontrollvolumen-Wände ![]() liegen zwischen den
Gitterpunkten
liegen zwischen den
Gitterpunkten ![]() . Der genaue Ort ist willkürlich.
Einige Praktiken werden später diskutiert. Der Ort wird hier einfach
als bekannt vorausgesetzt. Die Größen
. Der genaue Ort ist willkürlich.
Einige Praktiken werden später diskutiert. Der Ort wird hier einfach
als bekannt vorausgesetzt. Die Größen ![]() resultieren aus der
Quellterm-Linearisierung:
resultieren aus der
Quellterm-Linearisierung:
| (4.4) |
Die Profilannahmen waren ein stückweise lineares
![]() -Profil für den Gradienten
-Profil für den Gradienten
![]() und ein stückweise
konstantes Profil
und ein stückweise
konstantes Profil ![]() für den linearisierten Quellterm. Andere
Profile sind möglich und erlaubt, solange die vier Grundregeln nicht
verletzt werden.
für den linearisierten Quellterm. Andere
Profile sind möglich und erlaubt, solange die vier Grundregeln nicht
verletzt werden.
Es folgen einige weitere wichtige Gesichtspunkte des eindimensionalen Wärmeleitungsproblems.