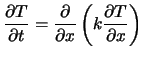 |
(4.27) |
Zunächst konzentrieren wir uns auf den instationären Term und lassen den Quellterm weg:
mit
![]() als Vorraussetzung, im Diffusionskoeffizient
mit 'verarbeitet'.
als Vorraussetzung, im Diffusionskoeffizient
mit 'verarbeitet'.
Die Zeit ist eine einseitig gerichtete Koordinate, also ist ein
Fortschreitungsverfahren in Zeitrichtung möglich:
Wir berechnen die Lösung
ausgehend von der Anfangsverteilung der Temperatur.
In einem typischen Zeitschritt: bei gegebenen Werten von ![]() zur Zeit
zur Zeit ![]() sind
sind
![]() -Werte zur Zeit
-Werte zur Zeit
![]() zu berechnen.
zu berechnen.
Es seien die alten Werte
![]() und die zur Zeit
und die zur Zeit
![]() sind
sind
![]() . Diskretisierungsgleichung
aus Integration von (4.27) über ein Kontrollvolumen
(z.B. Abbildung 10) und über ein Zeitintervall von
. Diskretisierungsgleichung
aus Integration von (4.27) über ein Kontrollvolumen
(z.B. Abbildung 10) und über ein Zeitintervall von ![]() bis
bis
![]() ist:
ist:
Als Profilannahme für die Zeitableitung verwenden wir: der Wert von ![]() gilt im
ganzen Kontrollvolumen, d.h.
gilt im
ganzen Kontrollvolumen, d.h.
![]() :
:
In Analogie zur stationären Wärmeleitung für
![]() setzen wir:
setzen wir:
Nun ist die Profilannahme für die zeitliche Veränderung von
![]() von
von ![]() bis
bis
![]() gesucht.
gesucht.
Allgemeine Darstellung
einiger Möglichkeiten für
![]() :
:
mit Wichtungsfaktor
![]() . Analoges gilt für die
. Analoges gilt für die ![]() -
und
-
und ![]() -Integrale.
-Integrale.
Man erhält:
Im folgenden wird der Index 1 weggelassen, d.h.
![]() sind Werte
zur Zeit
sind Werte
zur Zeit
![]() . Die Diskretisierungsgleichung lautet dann
. Die Diskretisierungsgleichung lautet dann
mit den Varianten Explizit, Crank-Nicolson und Voll Implizit:
 |
(4.34) |
Wir bevorzugen die voll implizite Variante.
Explizit ![]() ergibt für (4.33):
ergibt für (4.33):
Vor dem Hintergrund der 2. Grundregel ist zu beachten, daß der Koeffizient von
![]() in (4.35) negativ werden kann.
in (4.35) negativ werden kann.
Für ![]() und
und
![]() muß gelten
muß gelten
sonst können physikalisch unsinnige Ergebnisse entstehen. (4.36) ist ein bekanntes Stabilitätskriterium für das explizite Schema. Wir haben es hier abgeleitet aus physikalischen Überlegungen auf der Basis der vier Grundregeln.
Crank-Nicolson ist bedingungslos stabil. Das
bedeutet keineswegs, daß sich physikalisch realistische Ergebnisse
für beliebige Zeit- und Ortsschrittweiten ergeben! Oft ergeben sich
oszillierende Lösungen.
Das voll implizite Schema ist realitätsnäher als
das Crank-Nicolson-Schema, besonders für große ![]() .
.
Die Forderung nach stets positivem Koeffizienten von ![]() in (4.33) erzwingt
in (4.33) erzwingt ![]() . Ein voll implizites Schema ergibt immer
ein physikalisch sinnvolles Verhalten.
. Ein voll implizites Schema ergibt immer
ein physikalisch sinnvolles Verhalten.
Beachte: für kleine